Review question R8408 at the Geometry of Equations station
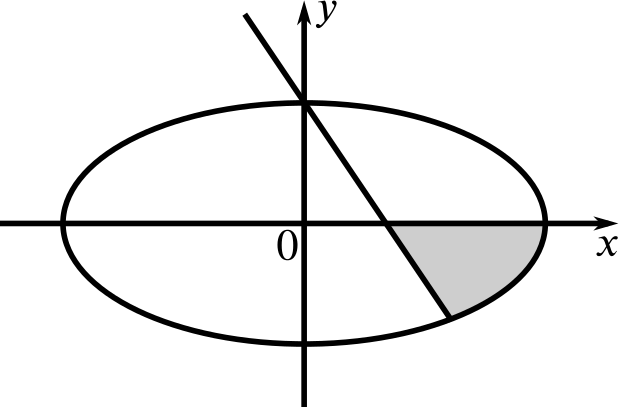
In Fig. 1 (not drawn to scale) the curve has equation \(x^2+4y^2=16\). The straight line has a gradient of \(-2\) and passes through the intersection of the curve with the positive \(y\)-axis.
Write down the three inequalities which are sufficient to define the shaded area (including the three lines bounding it).
Using this Review question
Students may well have familiarity with sketching the graphs of inequalities, but here they are required to work backwards and to determine the inequalities involved. This requires them to understand what an inequality means, and the elliptical boundary may well provide an opportunity to clarify areas of confusion.
This question also requires students to solve a coordinate geometry problem to find the equation of the straight line.
As generalisations or extensions, students could construct similar examples of their own for each other to solve, or could use inequalities to specify the other regions in the diagram.
Aspects of mathematical thinking
Mathematical behaviours to look out for
Testing the direction of an inequality by checking a point
Planning a solution strategy
Overarching ideas
- Generalising [and specialising]: how could the problem be generalised?
Common issues and misconceptions
- Thinking that “\(\le\)” means “below the line”

