How many regions are created by the graphs $y=x^3, y=x^4$ and $y=x^5$?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Ref: R5685

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Solution

Into how many regions is the plane divided when the following equations are graphed, not considering the axes?

\[y=x^3\]

\[y=x^4\]

\[y=x^5\]

$6$, (b) $7$, (c) $8$, (d) $9$, (e) $10$.

A careful sketch seems like our best plan, noting that all three curves go through $(0,0)$ and $(1,1)$, and that $x^3>x^4>x^5$ on the interval $0<x<1$.

We also have that $y=x^3$ and $y=x^5$ both go through $(-1,-1)$, and $x^3 < x^5 < 0$ on the interval $-1<x<0$.

So here is our sketch, without including the axes;

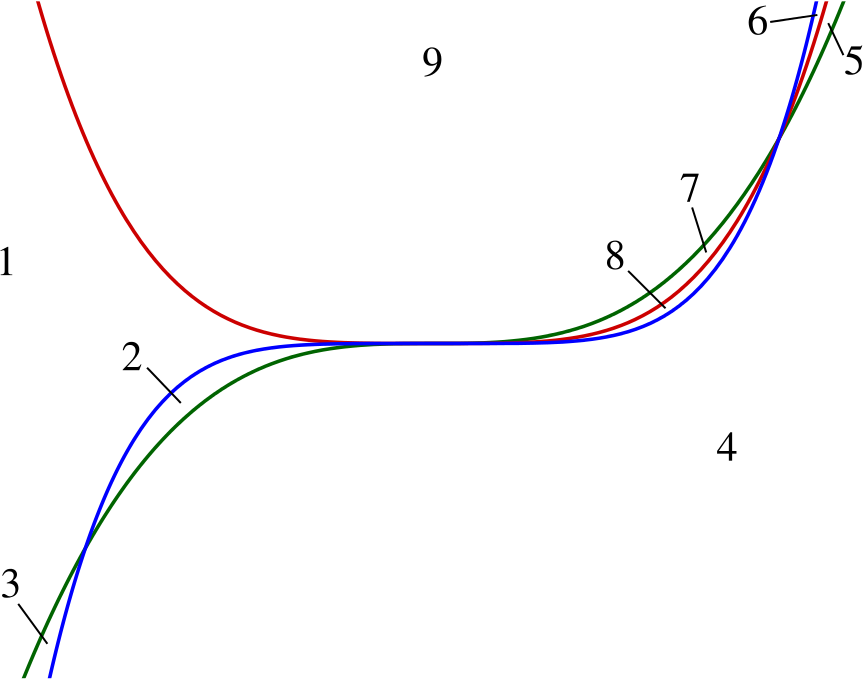
a sketch of the three curves y equals x cubed, y equals x to the power four, and y equals x to the power five

We have nine regions, and so the answer is (d).

Previous Next

Polynomials & Rational Functions

How many regions are created by the graphs $y=x^3, y=x^4$ and $y=x^5$? Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Solution

Station

Lines

How many regions are created by the graphs $y=x^3, y=x^4$ and $y=x^5$?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource