Express \(x^3 - 3x - 2\) as the product of three linear factors.
By the factor theorem, a polynomial \(f(x)\) has a linear factor \((x-a)\) if and only if \(f(a) = 0\).
If we let \(f(x) = x^3 - 3x - 2\), we have
| \(x\) | \(0\) | \(1\) | \(2\) |
|---|---|---|---|
| \(f(x)\) | \(-2\) | \(-4\) | \(0\) |
So \((x-2)\) is a factor of \(f(x) = x^3 - 3x - 2\), and \(f(x) = (x-2)(x^2+ax+1)\).
Since \(f(x)\) has no \(x^2\) term, \(a = 2\), and \(f(x)\) can be factorised completely as \[f(x) = (x-2)(x+1)^2,\] which is the product of three linear factors.
Show that \(x^3 - 3x - 2\) may also be expressed in the form \((x-1)^2(x+p) + q\), where \(p\) and \(q\) are constants to be found.
for some \(p\) and \(q\)?
By equating coefficients, we need \(p\) and \(q\) that satisfy \[\begin{align*} 0 &= p - 2, \\ -3 &= 1 - 2p, \\ -2 &= p + q \end{align*}\] simultaneously. The first gives us \(p = 2\), as does the second, and the third becomes \(q = -4\). So we can write down the identity \[\begin{equation*} x^3 - 3x - 2 = (x-1)^2(x+2) - 4. \end{equation*}\]Hence, or otherwise, show that the curve whose equation is \(y = x^3 - 3x - 2\) has a minimum point where \(x = 1\).
We know \(f(x) = (x-1)^2(x+2) - 4\). When \(x = 1\), \(f(x) = -4\).
When \(x =1 + \alpha\), where \(\alpha\) is small and positive, then \(f(x) = \alpha^2(3+\alpha)-4 > -4\).
When \(x = 1 - \alpha\), then \(f(x) = \alpha^2(3-\alpha)-4 > -4\). Thus \(y = f(x)\) has a minimum at \(x = 1\).
Or else we can differentiate. If \(y = f(x) = x^3 -3x -2\), then \(y' = 3x^2-3 = 0\) when \(x = 1\).
We have \(y'' = 6x = 6\) when \(x = 1\), which is positive, so we have a minimum.
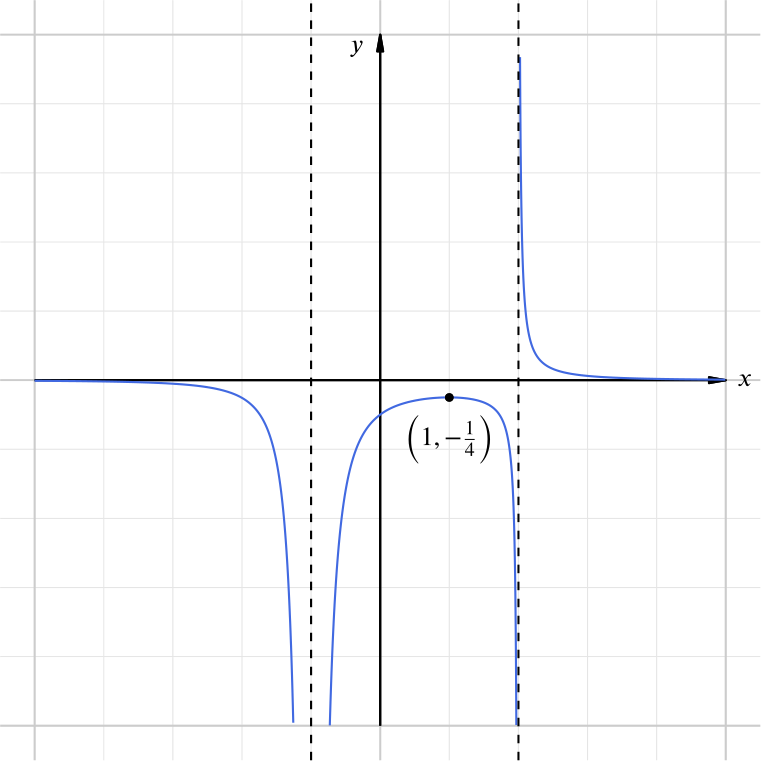
indicating clearly all its asymptotes.
In sketching the graph, we will ask four questions:
- what are the intercepts?
When \(x = 0\), \(y = -\dfrac{1}{2}\). This is the \(y\)-intercept of the curve. There are no \(x\)-intercepts, since the numerator of \(y\) can never equal zero.
- what is the asymptotic behaviour?
There are two vertical asymptotes (corresponding to the roots of the denominator) at \(x = -1\) and \(x = 2\).
Since the denominator of \(y\) tends towards \(\pm \infty\) as \(x\) tends towards \(\pm \infty\), and as the numerator is constant, we can see \(y \to 0\) as \(x \to \pm \infty\). Thus there is one horizontal asymptote, \(y = 0\).
- where is \(y\) positive and negative?
The sign of \(y\) depends wholly on the sign of \((x-2)\), since \((x+1)^2\) is never negative, and so \(y > 0\) if \(x > 2\) and \(y < 0\) if \(x < 2\) (provided that \(x \ne -1\)).
- are there any turning points?
Finally, the denominator has a local minimum at \(x = 1\), and so its reciprocal \(y\) must have a local maximum at \(x = 1\).
We can now sketch \(y\):
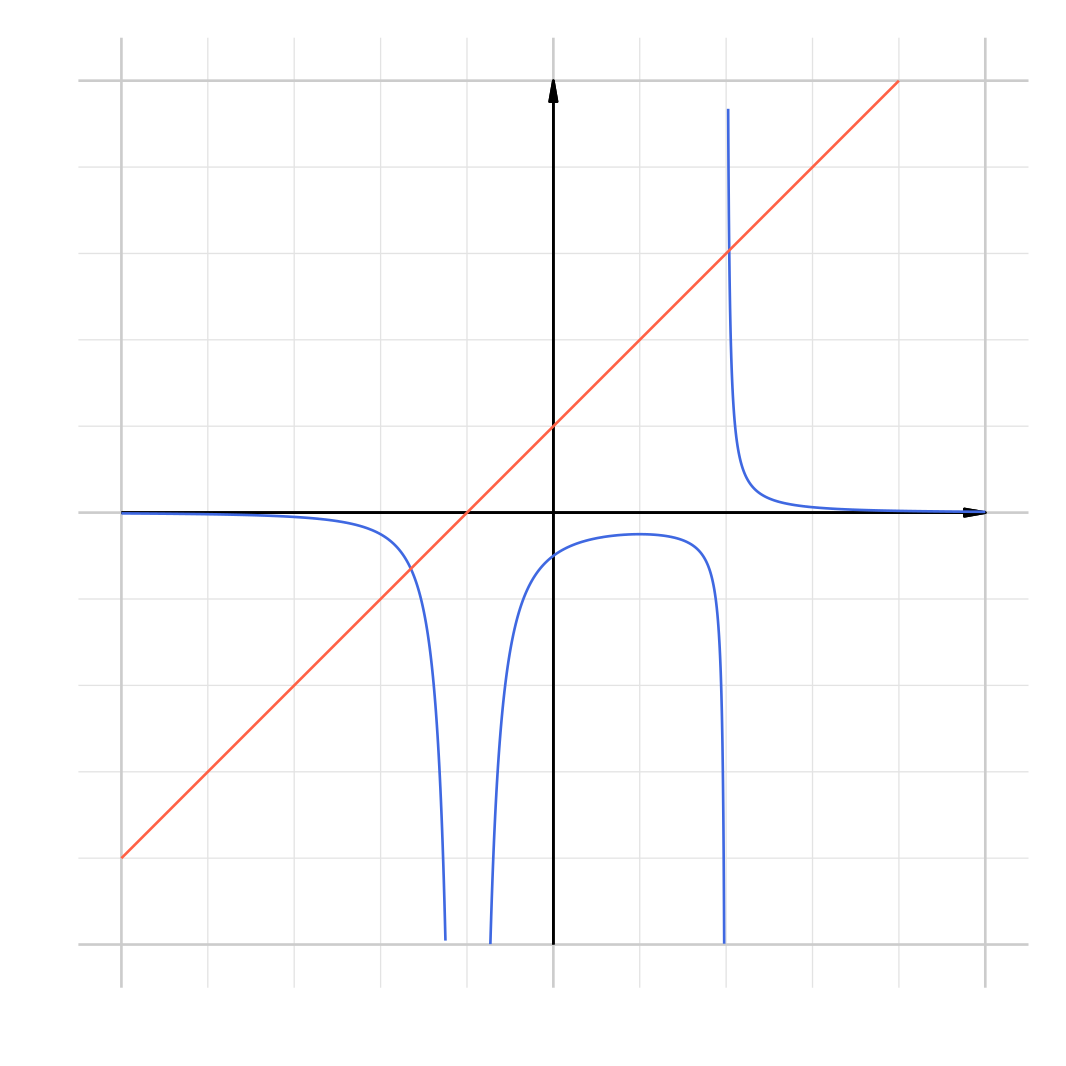
(Clearly \(x^3 - 3x - 2\) cannot be zero, since in this case the equation is not satisfied.) A real solution to this equation corresponds precisely to an intersection between the line \(y = x+1\) and the curve \(y = \dfrac{1}{x^3 - 3x - 2}\).
Thus we have this sketch of the line and the curve. There are two intersections, and hence there are two real roots to the equation.