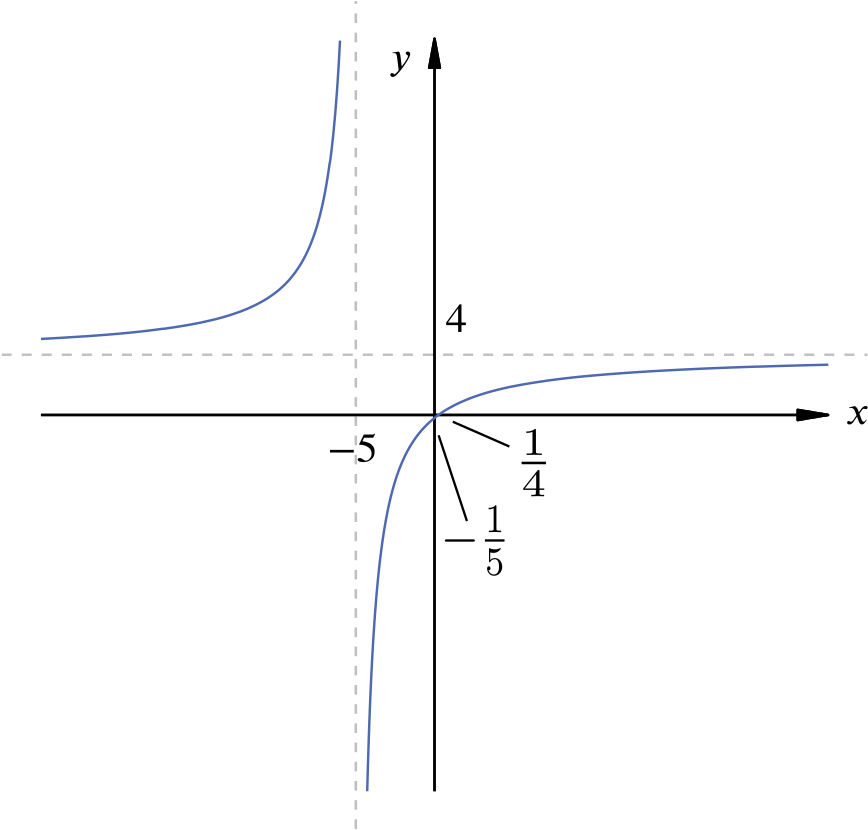
Can we sketch the graph of $y = (4x-1)/(x+5)$?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

In sketching the graph, we’ll look at four different features of the function:

1. its intercepts with the axes;
2. its asymptotic behaviour;
3. its signs in various regions; and
4. its turning points, if it has any.

Intercepts

The \(y\)-intercept is \[ y = y(0) = \frac{4 \times 0 - 1}{0+5} = -\frac{1}{5}. \]

The \(x\)-intercepts are the values of \(x\) such that \[ 0 = \frac{4x-1}{x+5}; \] there’s one such value, \(x = \dfrac{1}{4}\).

Asymptotic behaviour

There’s a single vertical asymptote when the denominator is zero, the line \(x = -5\).

If we rewrite the function as \[ \frac{4x-1}{x+5}=4-\frac{21}{x+5} \] it is easier to see that as \(x \to \infty\), \(y \to 4\) and that as \(x \to -\infty\), \(y \to 4\) so there’s a single horizontal asymptote, \(y = 4\).

Signs

The sign of \(y\) can only change when \(x\) moves across a vertical asymptote or an \(x\)-intercept.

The \(x\)-axis falls into three regions, \(x < -5\), \(-5 < x < \dfrac{1}{4}\), and \(x > \dfrac{1}{4}\), and in each of these regions \(y\) has a constant sign.

We can determine the sign of \(y\) in each of these regions by looking at the signs of the numerator and denominator separately.

• In the first region, \(4x - 1 < 0\) and \(x + 5 < 0\), so \(y\) is the quotient of two negative expressions, and is therefore positive.
• In the second region, \(4x - 1 < 0\) and \(x + 5 > 0\), and so \(y < 0\).
• In the third region, \(4x - 1 > 0\) and \(x + 5 > 0\), and so \(y > 0\).

Turning points

By considering the function in the form \[ \frac{4x-1}{x+5}=4-\frac{21}{x+5} \] we see that it is a transformation of \(y = \dfrac{1}{x}\). Therefore there are no turning points.

The sketch shows that we need the set of \(x\)-values from \(a\) to \(b\), where \(a\) is the solution of \(-1=\dfrac{4x-1}{x+5}\), and \(b\) is the solution to \(\dfrac{4x-1}{x+5}=1\).

We have \[\begin{align*} -1&=\dfrac{4x-1}{x+5}\\ &\implies -x-5=4x-1 \\ &\implies x = -\dfrac{4}{5}. \end{align*}\] and also \[\begin{align*} \dfrac{4x-1}{x+5}&=1 \\ &\implies 4x-1=x+5 \\ &\implies x = 2. \end{align*}\]

Thus \(a = -\dfrac{4}{5}\), and \(b = 2\), and the set of values for \(x\) that we need is \(\left\{ x \in \mathbb{R} : -\dfrac{4}{5}< x < 2 \right\}\).

Now \[ 3x^3 + 2x^2 + 6 \ge 19x \iff 3x^3 + 2x^2 - 19x + 6 \ge 0, \] so if we let \(p(x) = 3x^3 + 2x^2 - 19x + 6\), then we have to find the set of values of \(x\) for which \(p(x) \ge 0\).

Can we factor the polynomial \(p(x)\)?

By the factor theorem, \((x-a)\) is a factor of \(p(x)\) if and only if \(p(a) = 0\).

Let’s try a few different values for \(x\): every cubic equation has at least one real root, and if this is an integer, we have a chance of finding it here.

• \(p(0) = 6\);
• \(p(1) = 3 + 2 - 19 + 6 = -8\);
• \(p(2) = 3 \times 8 + 2 \times 4 - 19 \times 2 + 6 = 24 + 8 - 38 + 6 = 0\).

So our first factor is \((x-2)\). There are thus real constants \(\alpha\), \(\beta\) and \(\gamma\) such that \[\begin{align*} 3x^3 + 2x^2 - 19x + 6 = p(x) &= (\alpha x^2 + \beta x + \gamma)(x-2) \\ &= \alpha x^3 - 2\alpha x^2 + \beta x^2 - 2\beta x + \gamma x - 2\gamma \\ &= \alpha x^3 + (\beta - 2\alpha) x^2 + (\gamma - 2\beta) x - 2\gamma. \end{align*}\]

By equating coefficients, we have that \(\alpha = 3\), \(\gamma = -3\), and \(\beta - 2\alpha = 2\), i.e. \(\beta = 8\). Thus, \[ p(x) = (x-2)(3x^2 + 8x - 3). \] Factorising, we have \[ 3x^2 + 8x - 3 = (3x-1)(x+3). \] Therefore \[ p(x) = (x-2)(3x-1)(x+3). \]

The sign of \(p(x)\) can only change as \(x\) passes over a root of \(p(x)\); these roots are \(x = -3\), \(x = \dfrac{1}{3}\), and \(x = 2\).

This divides the \(x\)-axis into four regions.

• In the first region, with \(x < -3\), all three factors are negative, so \(p(x) < 0\).
• In the second region, with \(-3 < x < \dfrac{1}{3}\), two factors are negative and one is positive, so \(p(x) > 0\).
• In the third, with \(\dfrac{1}{3} < x < 2\), one factor is negative and two are positive, and so \(p(x) < 0\).
• Finally, with the fourth, with \(x > 2\), all three factors are positive and therefore \(p(x) > 0\).

We therefore have that \[ \{ x \in \mathbb{R} : p(x) \ge 0 \} = \{ x \in \mathbb{R} : x \ge 2 \} \cup \left\{ x \in \mathbb{R} : -3 \le x \le \frac{1}{3} \right\}. \]