Can we factorise $6x^3+5x^2-17x-6$ completely?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The remainder theorem tells us that if \(f(c)=r\) for some polynomial \(f(x)\), then \(r\) is the remainder when \(f(x)\) is divided by \(x-c\).

In our case, \(c\) is \(2\) for the first part, and \(-2\) for the second.

We can now substitute these values into \(f(x)\), giving

\[\begin{align*} f(+2)&=28,\\ f(-2)&=0. \end{align*}\]

Therefore the remainder when \(f(x)\) is divided by \(x-2\) is \(28\), and the remainder on dividing by \(x+2\) is \(0\).

Since the remainder of \(f(x)\) divided by \(x+2\) is zero, we know \(x+2\) is a factor of \(f(x)\).

We now know that \(f(x)\) is of the form \((x+2)(ax^2+bx+c)\), where \(a\), \(b\) and \(c\) are constants to be found. This means \[f(x) = 6x^3 + 5x^2 - 17x - 6 = (x+2)(ax^2+bx+c).\]

We can find \(a\), \(b\) and \(c\) by considering the coefficients of the different powers of \(x\).

The only cubic term on the right hand side is \(ax^3\), so we can see by comparing it with the left hand side that \(a = 6\).

The constant term is \(2c\), which must equal \(-6\), and so \(c = -3\).

There’ll be two square terms in the expansion of the right hand side, namely \(12x^2\) and \(bx^2\). Therefore \[\begin{align*} 12 + b &= 5 \\ \implies b &= -7. \end{align*}\] We can check this by looking at the linear terms; on the right hand side, we get \(2bx\) and \(-3x\), so \[\begin{align*} 2b - 3 &= -17 \\ \implies 2b &= -14 \\ \implies b &= -7, \quad \text{as above}. \end{align*}\]

Therefore we can write \(f(x) = (x + 2)(6x^2 - 7x - 3)\).

The quadratic bracket here can be factorised by inspection, or by using the quadratic formula if we’re stuck. We find that \[f(x) = (x + 2)(3x + 1)(2x - 3).\]

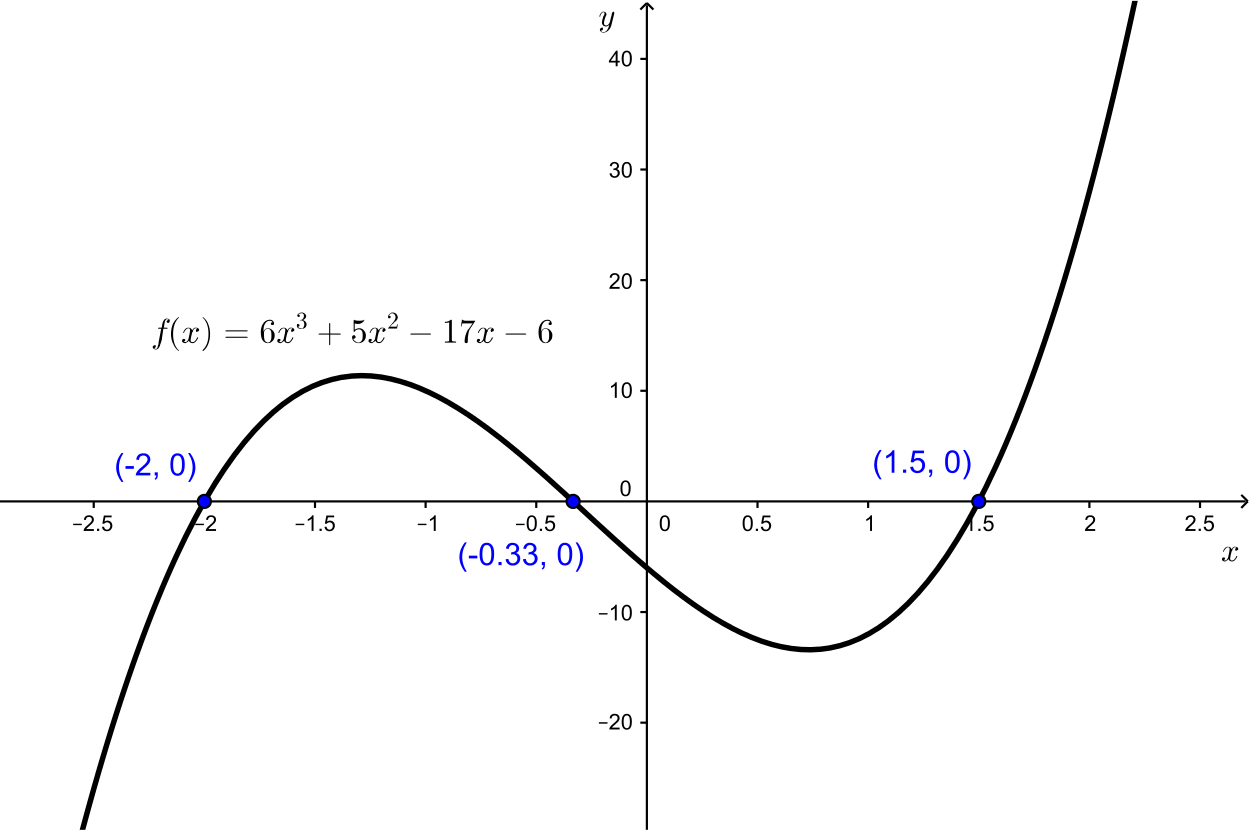
Although the question doesn’t ask for this, click below for a plot of \(y=f(x)\), with the three roots indicated.

Let’s factorise; \(x^2 + x - 6 = (x + 3)(x - 2)\).

So we know that \((x-2)\) and \((x+3)\) are factors of the above cubic expression, and so if we substitute in \(x=2\) or \(x=-3\) to this cubic, the result has to be zero.

This leads to the following pair of equations: \[\begin{align} 8a+2b+14&=0 \quad \implies \quad 4a + b + 7 = 0 \label{eq:I}\\ -27a-3b+9&=0 \quad \implies \quad -9a - b + 3 = 0. \label{eq:II} \end{align}\] We can solve these by adding them together: \[\begin{align*} -5a + 10 &= 0 \\ \implies a &= 2, \end{align*}\] and substituting into \(\eqref{eq:I}\), we find \[\begin{align*} 4 \times 2 + b + 7 &= 0 \\ \implies b &= -15. \end{align*}\]

We can check this by substituting both \(a\) and \(b\) into \(\eqref{eq:II}\): \[-9 \times 2 - (-15) + 3 = 0.\]

We therefore find \(a= 2\), \(b = 15\), and that the full cubic function is \(2x^3-x^2-15x+18\).