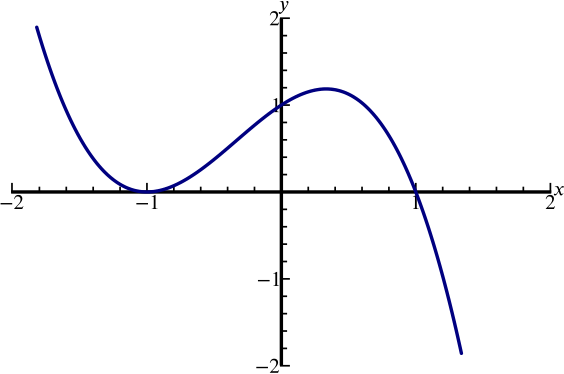
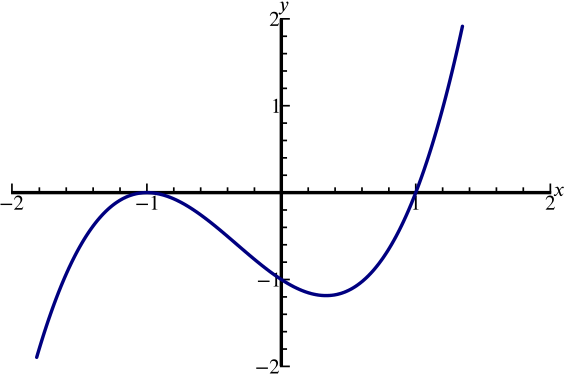
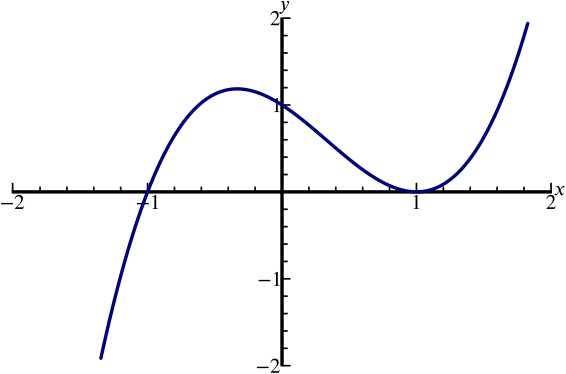
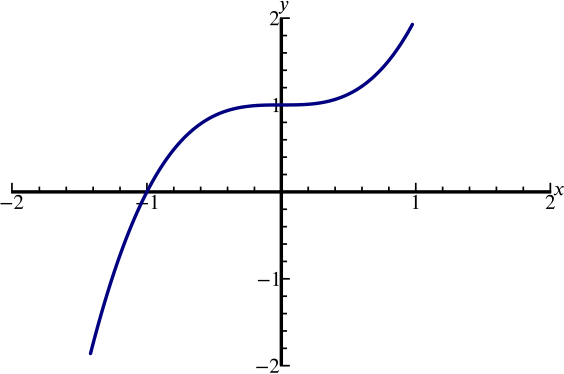
A sketch of the graph \(y=x^3-x^2-x+1\) appears on which of the following axes?
|
|
|
|
|
|
The coefficient of \(x^3\) is positive, so for large \(x\) we get a positive \(y\), in which case (a) cannot be the graph.
When \(x=0\), \(y=1\), so the \(y\)-intercept is \(+1\) and therefore (b) cannot be the graph.
We note that if \(x=1\) then \(y=0\), so the point \((1,0)\) is on the graph, which is not the case for (d).
Hence, the correct answer is (c).
Alternatively, we can factorise the graph into \(y=(x+1)(x-1)^2\), using the Factor Theorem.
This curve cuts the \(x\)-axis at \(-1\), and touches it at \(1\). Hence, the correct answer is (c).