Given a positive integer \(n\) and a real number \(k\), consider the following equation in \(x\), \[(x-1)(x-2)(x-3) \times \cdots \times (x-n) = k.\] Which of the following statements about this equation is true?
- If \(n=3\), then the equation has no real solution \(x\) for some values of \(k\).
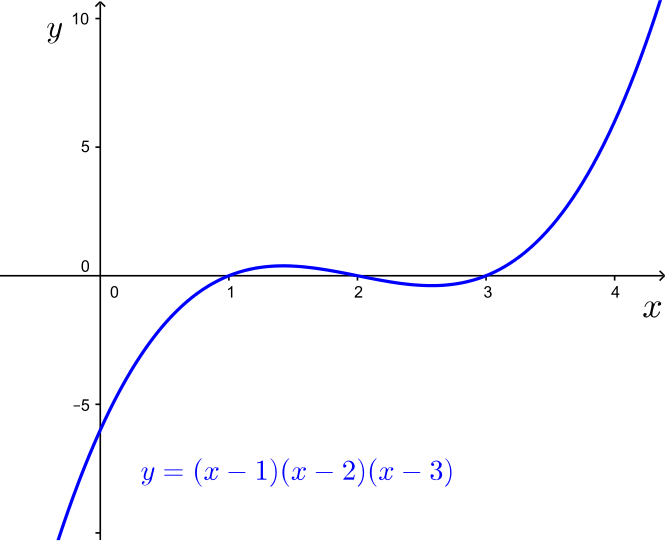
If \(n=3\), we have the equation \((x-1)(x-2)(x-3) = k\), which is a cubic function in \(x\).
We know from the shape of cubics that the function will take on all real values, and so (a) is untrue.
Useful fact: every cubic equation with real coefficients has at least one real root.
- If \(n\) is even, then the equation has a real solution \(x\) for any given value of \(k\).
If \(n\) is even, then the leading term of the function will be a positive even power of \(x\), such as a quadratic (\(n=2\)) or a quartic (\(n=4\)) function.
We know from the shape of these functions that they have a finite minimum value.
Thus the equation will not have a solution for sufficiently negative values of \(k\).
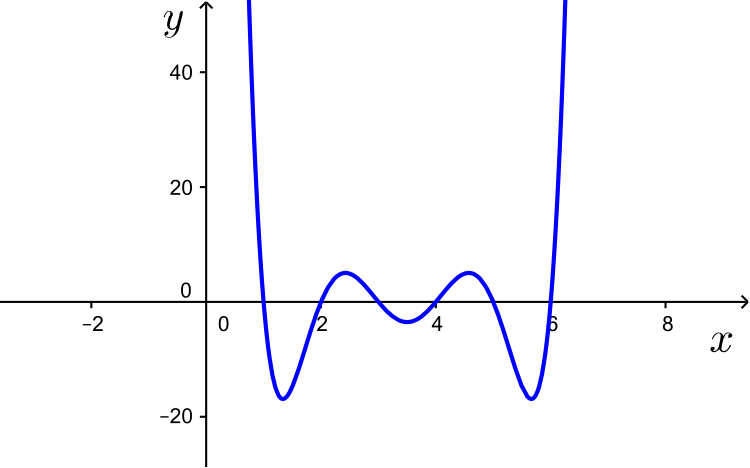
Hence (b) is untrue.
- The equation never has a repeated solution \(x\) for any given values of \(k\) and \(n\).
If we set \(n=2\), we have \((x-1)(x-2) = k\), i.e. \(x^2 - 3x + (2-k)=0\). Completing the square gives \[\left(x-\frac{3}{2}\right)^2 -\left(\frac{1}{4} + k\right) = 0,\] so if we set \(k = -\dfrac{1}{4}\), then the equation has a repeated root at \(x = \dfrac{3}{2}\).
Another way of thinking about this is that when \(n=2\), the graph \(y=(x-1)(x-2)\) is a parabola, so it has a minimum point.
When \(y=k\) touches the graph at this minimum point, there will be a repeated root, and so this curve is a counter-example to (d).
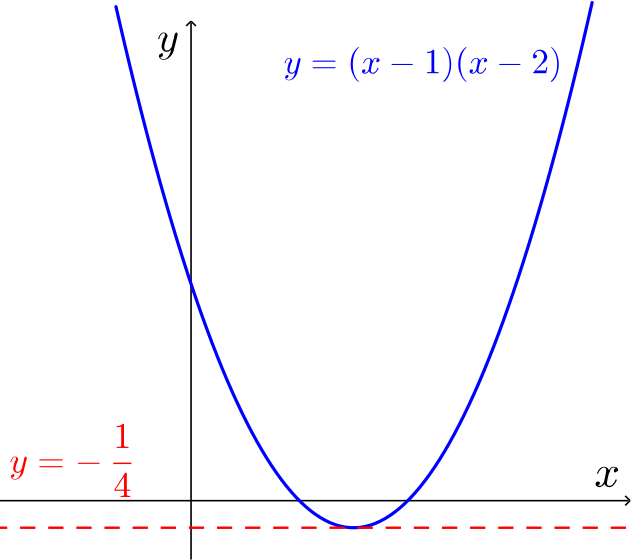
Hence (d) is untrue, and by process of elimination, the answer is (c).
We can also show that (c) is true directly.
- If \(k \ge 0\) then the equation has (at least) one real solution \(x\).
If we let \[f(x) = (x-1)(x-2)(x-3) \times \cdots \times (x-n)\] then \(f(n) = 0\).
If we then increase \(x\) from \(n\), \(f(x)\) also increases from \(0\), since every term in the product is positive and increasing.
Hence \(f(x)\) will take every positive real value for \(x>n\), and so the equation will have some solution for every \(k\ge0\), so (c) is true.
This is also clear from the shape of the graphs of \(y=f(x)\).

