Can we find the coefficients and factorise this quartic?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Substituting \(x=-\frac{1}{2}\) we have \[\begin{align*} f\left(-\frac{1}{2}\right) &= 0\\ \implies\quad \frac{2}{16}-\frac{a}{8}+\frac{b}{4}+2-4 &= 0\\ \iff\quad 1 - a + 2b - 16 &= 0\\ \iff\quad -a+2b &= 15 \end{align*}\] Also we have that \[\begin{align*} f(2) &= 0\\ \implies\quad 32+8a+4b-8-4 &= 0\\ \iff\quad 2a+b &= -5 \end{align*}\]

We now have two simultaneous equations in \(a\) and \(b\). If we add twice the first to the second, to eliminate \(a\), we see that \(5b = 25\) and so \(b = 5\).

We can then use either equation to find that \(a = -5\).

Since \(f\left(-\frac{1}{2}\right)=0\) and \(f(2)=0\) we know that \(2x+1\) and \(x-2\) are two factors of \(f(x)\).

So \[f(x)=2x^4 - 5x^3 + 5x^2 - 4x - 4 =(2x+1)(x-2)g(x) = (2x^2 - 3x -2)g(x),\] where \(g(x)\) is a quadratic polynomial. By inspection, we can see that \(g(x)=x^2-x+2\).

Therefore we have \[f(x)=(2x+1)(x-2)(x^2-x+2).\]

To show that \(f(x)\) only has two real roots we need to show that \(g(x)=x^2-x+2\) has no real roots.

The discriminant of \(g(x)\) is \(1 - 4 \times 2 = -7\), and since this is negative, we see that \(g(x)\) has no real roots.

So, we can conclude that \(f(x)\) has exactly two real roots, which are \(x=-\dfrac{1}{2}\) and \(x=2\).

If we sketch the graph of \(f(x)\), we’ll clearly see the regions for which \(f(x)>0\). We know that there are only two real roots, and we observe that the \(y\)-intercept is \(-4\).

So the graph is

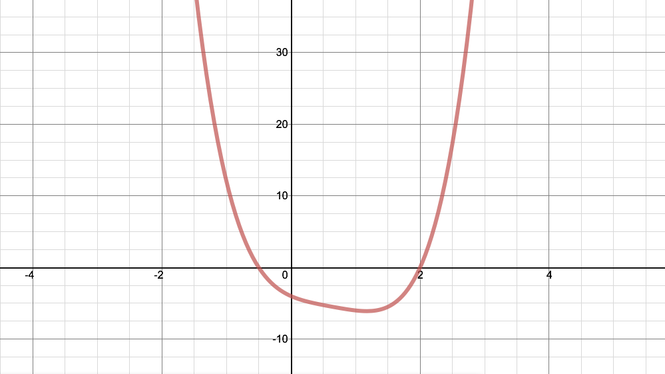
From this, we can see that the values of \(x\) for which \(f(x)>0\) are \(x<-\dfrac{1}{2}\) and \(x>2\).