The equation \[(x^2+1)^{10} = 2x - x^2 - 2\]
has \(x=2\) as a solution;
has no real solutions;
has an odd number of real solutions;
has twenty real solutions.
We can complete the square on the right-hand side of the equation to give \[(x^2+1)^{10} = -1 - (x-1)^2.\]
Now for real \(x\), the left-hand side of this equation is always positive, but the right-hand side is always negative, so the equation has no real solutions.
Therefore the answer is (b).
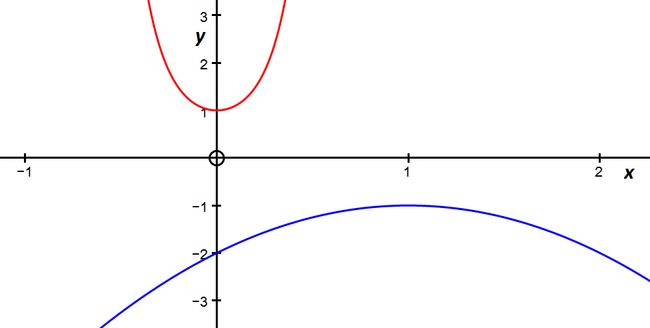
The graphs of \(y=(x^2+1)^{10}\) and \(y= -1 - (x-1)^2\) help us to see what is going on.