Graphical Approach
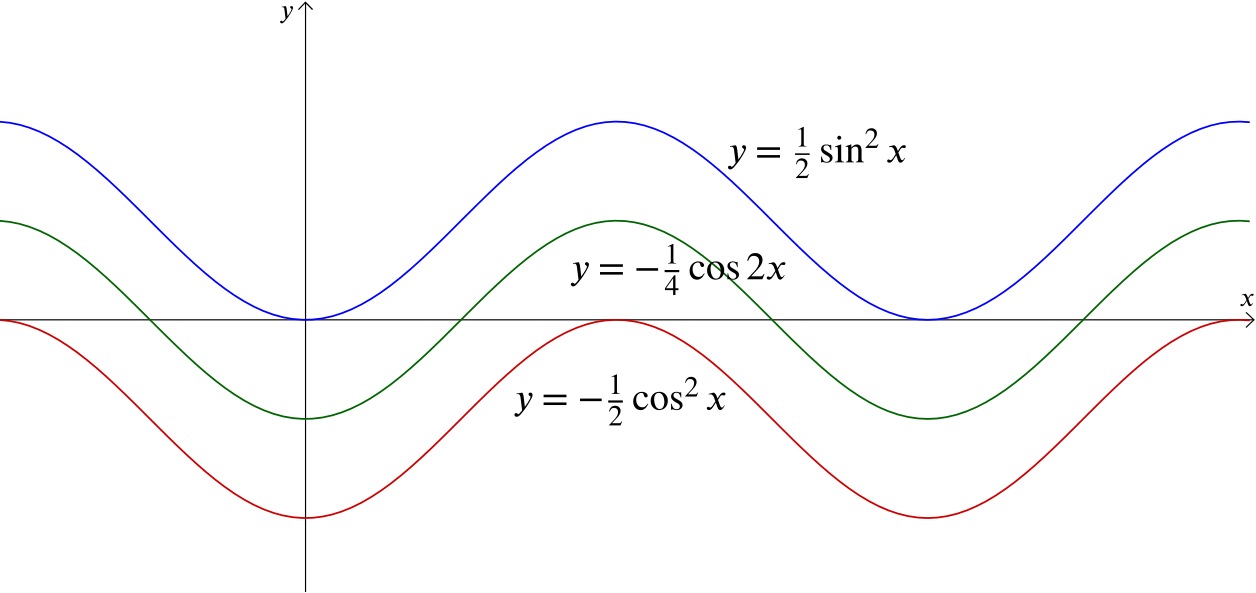
From the graphs we can see that each is a translation parallel to the \(y\)-axis of the same curve. Therefore we can add a constant value to each function and get the other solutions.
We used the same symbol, \(C\) for the constant of integration in each case, but in fact they must be different constants.
Algebraic Approach
If the constants are different, let’s call them \(P\), \(Q\) and \(R\) rather than \(C\).
So we have the three answers as:
| \(-\dfrac{1}{4} \cos(2x) + P\) | \(-\dfrac{1}{2} \cos^2 (x) + Q\) | \(\dfrac{1}{2} \sin^2(x) + R\) |
Are there any trigonometric identities that connect the trigonometric functions?
We know that \(\cos(2x) \equiv 2\cos^2(x)-1 \equiv 1-2\sin^2(x)\) and \(\cos^2(x) \equiv 1-\sin^2(x)\).
Therefore, \[-\dfrac{1}{4} \cos(2x) + P = -\dfrac{1}{4} (2\cos^2(x)-1) +P = -\dfrac{1}{2} \cos^2(x) + \dfrac{1}{4} + P.\]
Comparing \(-\dfrac{1}{2} \cos^2(x) + \dfrac{1}{4} + P\) to \(-\dfrac{1}{2} \cos^2 (x) + Q\) we can see they are the same except for the constants. If we equate them then \(Q=\dfrac{1}{4} +P\).
Similarly, \[-\dfrac{1}{4} \cos(2x) + P = -\dfrac{1}{4} (1-2\sin^2(x)) +P = \dfrac{1}{2} \sin^2(x) - \dfrac{1}{4} + P.\]
Comparing again, we can see \(R=-\dfrac{1}{4} +P\)
So we can see the constant is not the same but the functions are equivalent.
How are the differences in the constants related to the translations of the graphs?
We worked out the integral in three different ways and got what at first seemed to be different answers. What would happen if we used the different methods to evaluate a definite integral such as \[\displaystyle{\int_0^{\pi/2} {\cos (x) \sin (x)} \, dx}\text{ ?}\]

