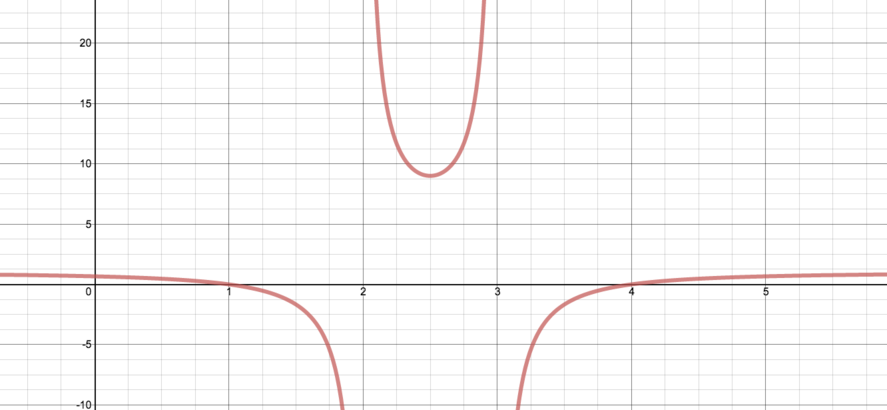
Sketch the curve \[y=\frac{(x-1)(x-4)}{(x-2)(x-3)}\]…
First, let’s think about the sign of \(y\) for various values of \(x\).
When \(x=1\) or \(x=4\), we have \(y=0\). When \(x=2\) or \(x=3\), we see that \(y\) is undefined—the graph has vertical asymptotes at these \(x\)-values.
For all other \(x\)-values, \(y\) is either strictly positive or strictly negative. The sign of \(y\) is determined by the sign of \(x-1\), \(x-2\), \(x-3\) and \(x-4\):
| Range of x-values | Sign of \(y\) |
|---|---|
| \(x<1\) | \(y>0\) |
| \(1< x <2\) | \(y<0\) |
| \(2< x <3\) | \(y>0\) |
| \(3< x <4\) | \(y<0\) |
| \(4< x\) | \(y>0\) |
As \(x \rightarrow \pm \infty\), the second term on the right tends to zero, and so \(y\) tends to \(1\).
We can look at the derivative of \(y\) to see whether the graph has any stationary points. Using the quotient rule to differentiate the expression above for \(y\), we have \[\frac{dy}{dx}=\frac{2(2x-5)}{(x^2-5x+6)^2}.\]
This is zero exactly when \(x=\dfrac{5}{2}, y = 3\). As \((x^2-5x+6)^2\) is always non-negative, we can see that \(\dfrac{dy}{dx}\) is negative for \(x<\dfrac{5}{2}\), \(x\neq 2\) and that \(\dfrac{dy}{dx}\) is positive for \(x>\dfrac{5}{2},\) \(x\neq 3\).
The curve can be written as \(y=\dfrac{\left(x-\frac{5}{2}\right)^2-\left(\frac{3}{2}\right)^2}{\left(x-\frac{5}{2}\right)^2-\left(\frac{1}{2}\right)^2}\), and so is symmetrical about \(x = \dfrac{5}{2}\).
We can now sketch the graph of this function.
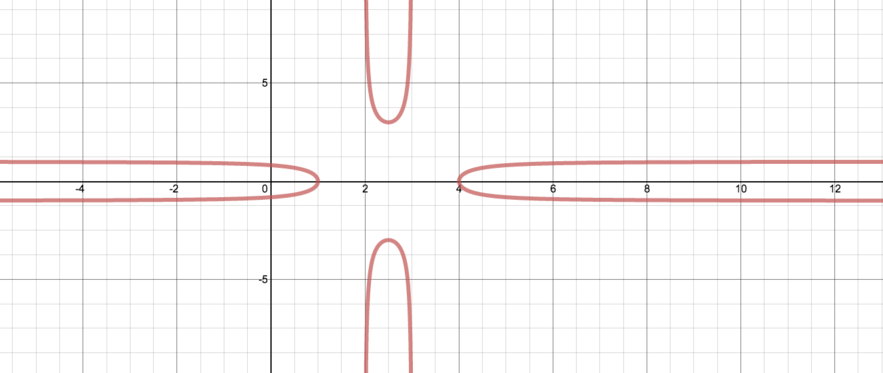
…and also, using this curve if you wish and explaining your argument carefully, the curve \[y^2=\frac{(x-1)(x-4)}{(x-2)(x-3)}.\]
The variable \(y\) is defined here only for values of \(x\) for which \(\dfrac{(x-1)(x-4)}{(x-2)(x-3)}\) is defined and non-negative, since \(y^2\) must be positive.
Also note that if \(\dfrac{(x-1)(x-4)}{(x-2)(x-3)}\) is defined and positive, the equation \(y^2=\dfrac{(x-1)(x-4)}{(x-2)(x-3)}\) has two solutions in \(y\)—one the negative of the other, so the graph will be symmetrical about the \(x\)-axis.
We can also think about, for a particular \(x\)-value, whether the (positive) \(y\)-value at this point is larger or smaller in the second graph than in the first.
The positive \(y\)-value in the second graph is simply the square root of the \(y\)-value in the first.
So, if the \(y\)-value in the first graph is greater than \(1\), it will be smaller at this point in the second graph.
If the \(y\) value in the first graph is between \(0\) and \(1\), it will be greater in the second graph. If it is either \(0\) or \(1\), it is unchanged.
What about the gradient of this graph? We have \[y^2=\frac{(x-1)(x-4)}{(x-2)(x-3)}.\]
Differentiating implicitly with respect to \(x\) gives us
\[2y \frac{dy}{dx} = \frac{2(2x-5)}{(x^2-5x+6)^2}.\]
What happens at \(x=1\) and \(x=4\) here? We have \(y=0\), and so \(\dfrac{dy}{dx}\) is undefined, which means that the graph is vertical at these \(x\)-values.
We can now sketch a graph of the function \(y^2=\dfrac{(x-1)(x-4)}{(x-2)(x-3)}\).