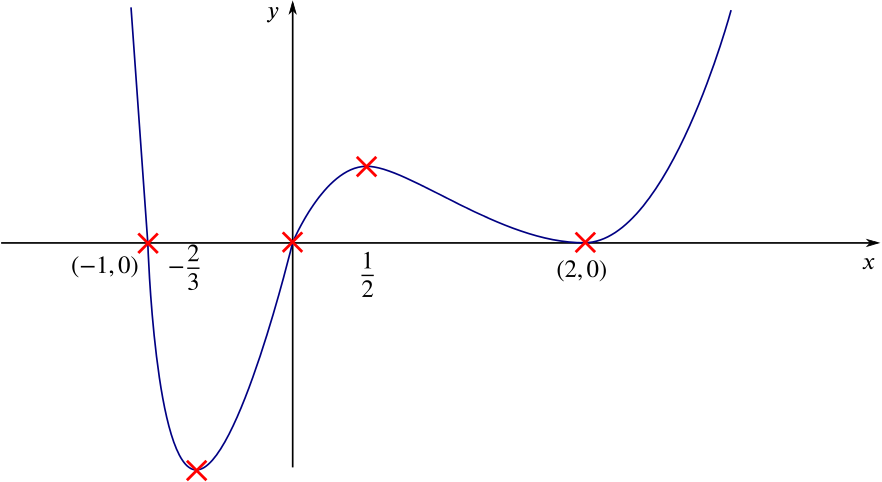
The curve \(C\) has equation \[y=x(x+1)(x-2)^4.\] Show that the gradient of \(C\) is \((x-2)^3(6x^2+x-2)\) and find the coordinates of all the stationary points.
To find the \(x\) coordinates of the stationary points we solve \[\frac{dy}{dx}=(x-2)^3(6x^2+x-2)=0 = (x-2)^3 (3x+2)(2x-1),\] which has solutions given by \[x=2 \text{ or } x=-\frac{2}{3} \text{ or } x=\frac{1}{2}.\] Substituting these values back in to \(y\) we find the stationary points of \(C\) are at \[(2,0), \left(\frac{1}{2}, \frac{243}{64}\approx 3.8\right), \left(-\frac{2}{3}, -\frac{8192}{729}\approx-11.2\right).\]
Determine the nature of each stationary point and sketch \(C\).
As this function is a degree six polynomial (sextic) with positive coefficient of \(x^6\) we know that for \(x\) large and negative it is decreasing, and for \(x\) large and positive it is increasing. Between these values the curve undulates so the first and last stationary points must be minima and the middle one a maximum.
Alternatively we could calculate the gradient at the integer values \(x= -1, \: 0, \: 1, \:\) and \(\: 3\) to verify the nature of the points.
We also know where all the \(x\) intercepts are, and have calculated the stationary points: joining the dots gives us a sketch of our curve.
To determine the nature of the stationary point, we might be tempted to differentiate again and find the sign of this at the points where \(\dfrac{dy}{dx} = 0\): \[\frac{d^2y}{dx^2}=3(x-2)^2(6x^2+x-2)+(x-2)^3(12x+1).\]
If we choose to do this we should notice that if \(\dfrac{dy}{dx} = 0\), then the first term here is bound to be zero, which reduces the workload, but is still more effort than necessary.
We might also think that at \(x=2\) there is a point of inflection because \(\frac{d^2y}{dx^2}=0\) here. We can see from the expression for \(y\) that the curve has a quadruple root at \(x=2\), so we expect the curve to touch the \(x\) axis here. (Note that a triple root would indicate a point of inflection.)
In separate diagrams draw sketches of the curves whose equations are:
\(y^2=x(x+1)(x-2)^4\);
\(y=x^2(x^2+1)(x^2-2)^4\).
In each case, you should pay particular attention to the points where the curve meets the \(x\) axis.
To sketch the graph of (i), first notice that we must have \(x(x+1)(x-2)^4 \geq 0\) in order for \(y\) to take real values. This means that (i) is not defined for the region \(-1 < x <0\).
The \(x\)-intercepts are the same, and the general shape will be similar to our first graph.
The difference is that every original \(y\)-value needs to be square-rooted for this graph, which will therefore be symmetrical about the \(x\) axis. This leads us to

For sketch (ii), first notice that the roots for \(y = 0\) have changed, that is, the \(x\)-intercepts will be different.
Also, notice that \(y\geq 0\) for all \(x\), and that we will have symmetry about the \(y\) axis, since swapping \(-x\) for \(x\) gives the same \(y\)-value. .
We see that the roots are at \(x=0\) and \(x=\pm\sqrt{2}\), and now we have all we need to sketch the graph.