If \[y=\frac{x(x-3)}{x-4}\] and \(x\) is real show that \(y\) cannot take any value between \(+1\) and \(+9\).
Approach 1: Using the Discriminant
Multiplying through by the denominator and rearranging, we get \[x^2-(y+3)x+4y=0.\]
Since \(x\) is real, this must have real roots. Therefore its discriminant is non-negative, that is \[(y+3)^2-16y\ge0.\] Solving this inequality, we find \[\begin{align*} &&(y+3)^2-16y &{}\geq 0&&\quad \\ \iff \quad&&y^2+6y+9-16y &{}\geq 0 \\ \iff \quad&&y^2-10y+9 &{}\geq 0 \\ \iff \quad&&(y-9)(y-1) &{}\geq 0, \end{align*}\]so we must have \(y \geq 9\) or \(y\leq1\), as we can see from this sketch.

Approach 2: Using calculus
We can find the stationary points of the function by differentiating.
Using the Quotient Rule, we have \[\begin{align*} \frac{dy}{dx}&{}=\frac{(2x-3)(x-4)-x(x-3)}{(x-4)^2}\\ &{}=\frac{x^2-8x+12}{(x-4)^2}\\ &{}=\frac{(x-2)(x-6)}{(x-4)^2}. \end{align*}\]So there are stationary points at \((2,1)\) and \((6,9)\).
Around \(x=2\), we have the points \((1,\frac{2}{3})\) and \((3,0)\), so \((2,1)\) is a local maximum.
Around \(x=6\), we have the points \((5,10)\) and \((7,\frac{28}{3})\), so \((6,9)\) is a local minimum.
Combining these with the observation that \(x=4\) is an asymptote, we can see that \(y\le1\) when \(x<4\) and \(y\ge9\) when \(x>4\).
Sketch the curve \(y=\dfrac{x(x-3)}{x-4}\).
We have an asymptote at \(x=4\), since the denominator is zero there.
To identify where the function is positive and negative, we note that it is the product and quotient of the three terms \(x\), \(x-3\)and \(x-4\).
| Range | \(x\) | \(x-3\) | \(x-4\) | \(y\) |
|---|---|---|---|---|
| \(x<0\) | \(-\) | \(-\) | \(-\) | \(-\) |
| \(0<x<3\) | \(+\) | \(-\) | \(-\) | \(+\) |
| \(3<x<4\) | \(+\) | \(+\) | \(-\) | \(-\) |
| \(x>4\) | \(+\) | \(+\) | \(+\) | \(+\) |
To find the intercepts, we note that when \(x=0\), \(y=0\). And when \(y=0\), we require \(x(x-3)=0\), so \(x=0\) or \(x=3\).
To find out how the function behaves as \(x\rightarrow \pm \infty\), we perform the division: \[\frac{x(x-3)}{x-4}=\frac{x^2-3x}{x-4}=x+1+\frac{4}{x-4},\] so as \(x\to\pm\infty\), \(y\approx x+1\), and we have an oblique asymptote.
We found above the stationary points at \((2,1)\) and \((6,9)\).
We can now put the above together to sketch the graph.
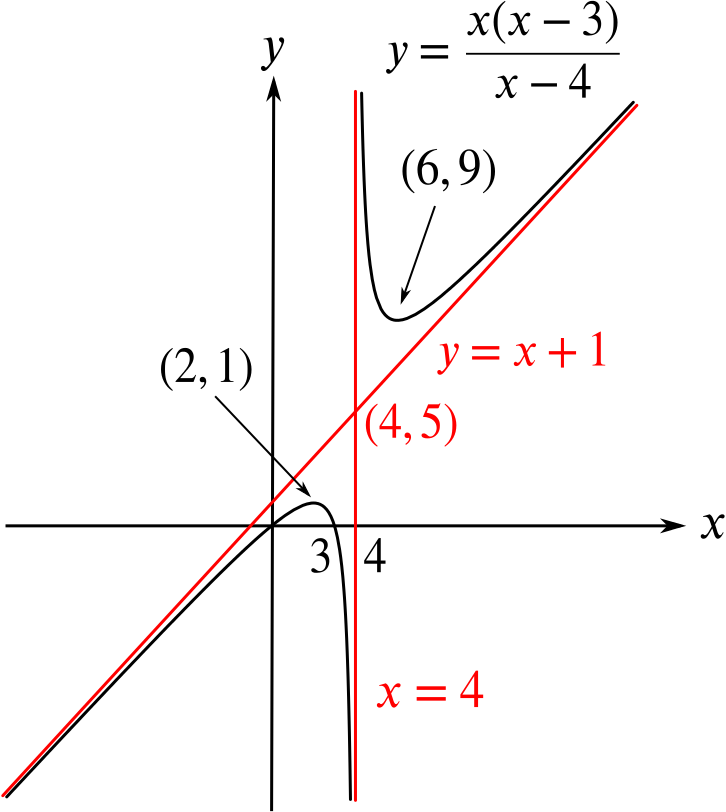
It is interesting to note that our graph appears to have rotational symmetry about the intersection of the two asymptotes, at \((4,5)\).
note that \((2,1)\) rotates to \((6,9)\), for example. How could we prove that the graph really does have rotational symmetry?
Using the same axes, sketch the curve \(y=\dfrac{5}{x}\) and find its intersection with the line \(x=4\).
The intersection of the curves \(y=\dfrac{5}{x}\) and \(x=4\) is \(\left(4,\dfrac{5}{4}\right)\).
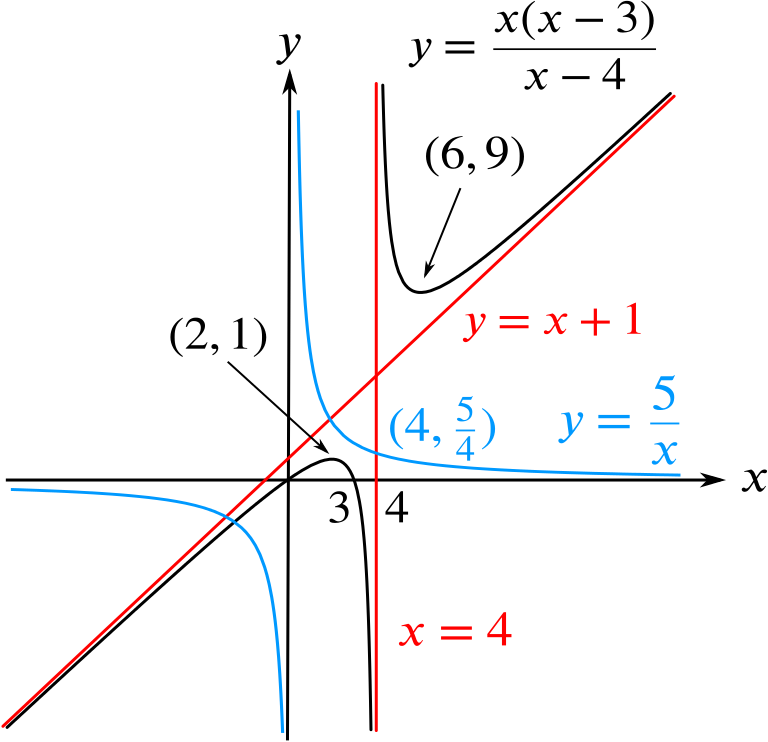
Hence prove that the equation \[\frac{5}{x}=\frac{x(x-3)}{x-4}\] has no positive root.
From the graph, it appears that solving \(y = \dfrac{5}{x}\) with \(y=\dfrac{x(x-3)}{x-4}\) simultaneously gives one negative root, but no positive ones.
For \(x<4\), we have \(\dfrac{5}{x}>\dfrac{5}{4}\), while we know from above that \(\dfrac{x(x-3)}{x-4}\le 1<\dfrac{5}{4}\), so there is no root with \(0<x<4\).
Similarly, for \(x>4\), we have \(\dfrac{5}{x}<\dfrac{5}{4}\), while \(\dfrac{x(x-3)}{x-4}\ge 9>\dfrac{5}{4}\), so there is no root with \(x>4\).
Clearly \(x = 4\) is not a root.
Hence the equation \(\dfrac{5}{x}=\dfrac{x(x-3)}{x-4}\) has no positive roots.

