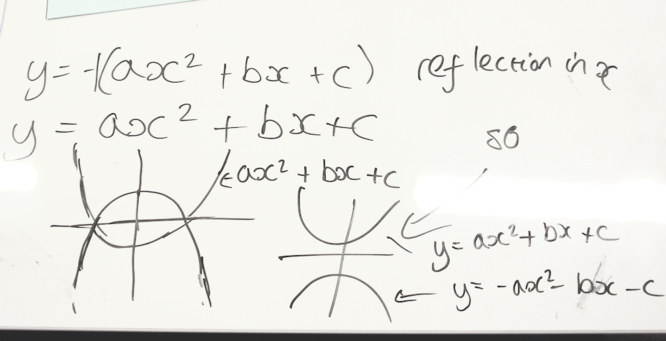Resources in action
Resource in action

Discriminating - teacher support
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Printable/supporting materials Printable version Fullscreen mode
Associated resource
Discriminating

Sample work

This sample work is provided to help prompt discussion and encourage students to reflect on alternative approaches.

Please note that to give you more flexibility in how you use the sample work, there is an extra printable copy without questions.

Card 1

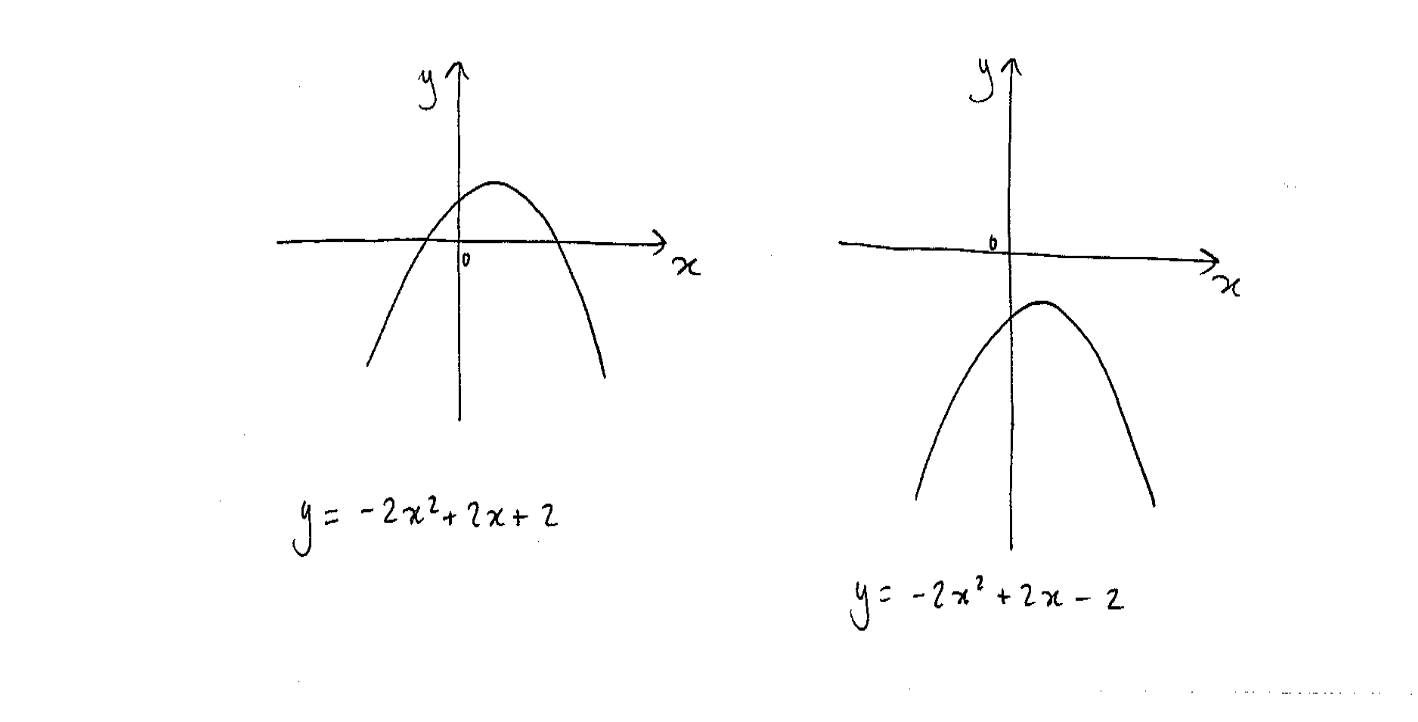
Two hand-drawn graphs showing a parabola crossing the x-axis twice and another that does not cross the x-axis

  • What do these graphs tell you about the statement on card 1?

  • What do these examples tell you about the statement on card 3?

Card 3

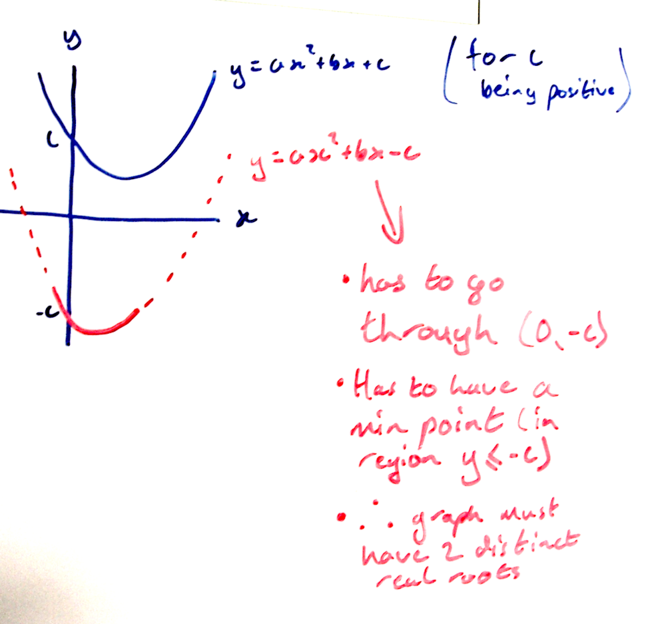
Two hand drawn parabolas where the first does not cross the x-axis and has a y-intercept of +c and the second crosses the x-axis twice and has a y-intercept of -c

  • Are there any other cases to be considered?

  • Can you use the discriminant to explain what you see in these graphs?

Card 4

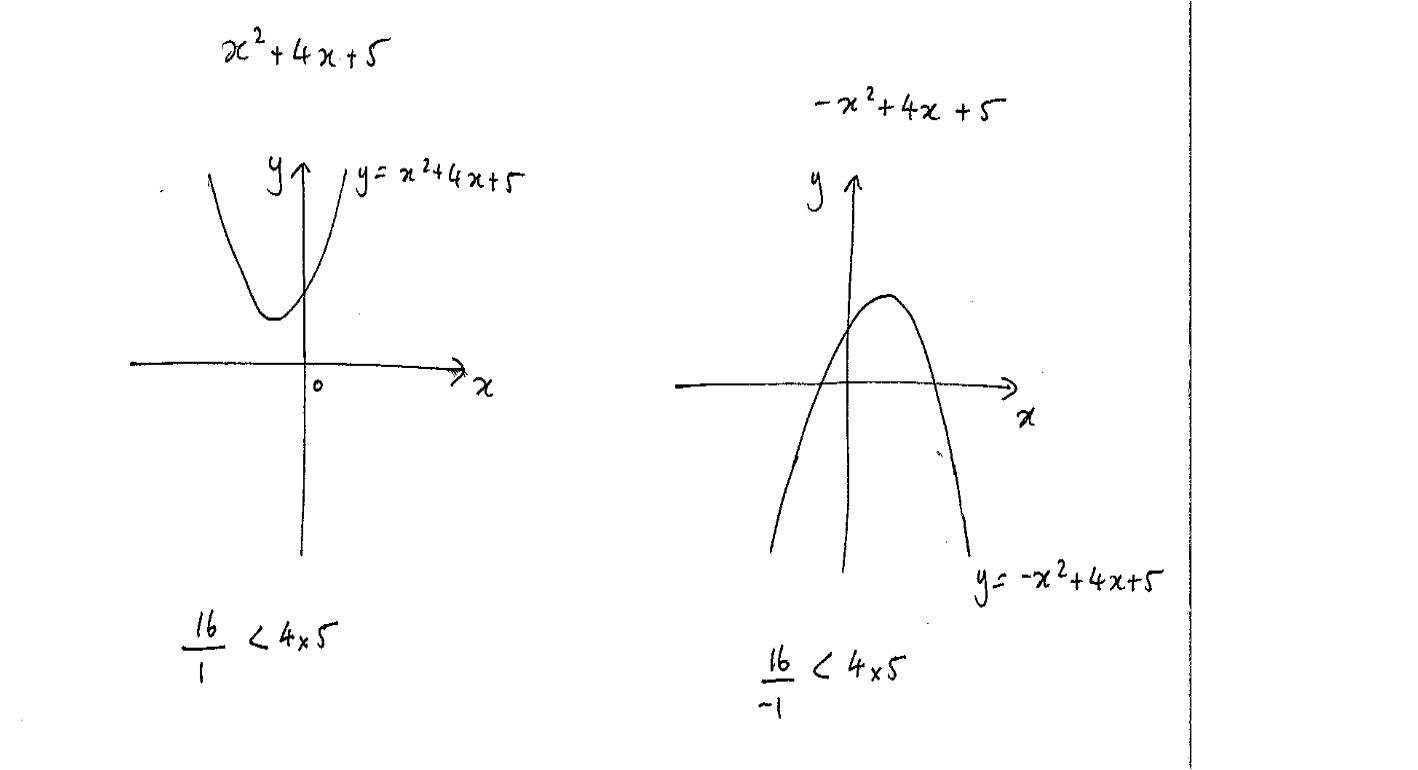
Two hand-drawn graphs showing a parabola that does not cross the x-axis and another that crosses the x-axis twice

  • Based on these examples, would you choose MUST, MAY or CAN’T for this statement?

  • Can you relate this to the discriminant?

  • Why has this student chosen two examples?

Card 5

Three hand-drawn parabolas where the first does not cross the x-axis and has a y-intercept of +c, the second crosses the x-axis at one point and c=0 and the third is a negative parabola which does not cross the x-axis and has a y-intercept of -c
  • What do these graphs tell you about the statement on card 5?

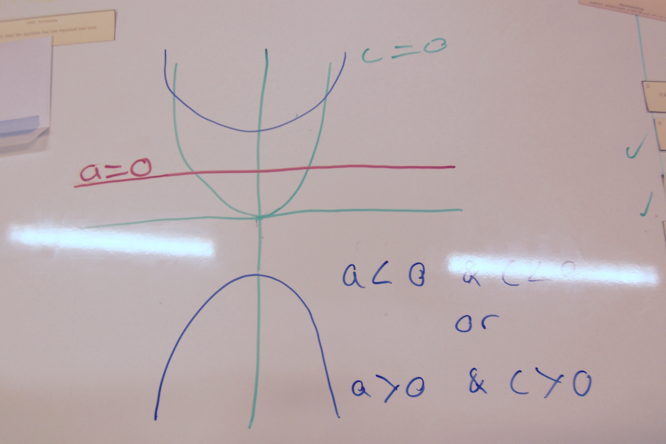
Card 7

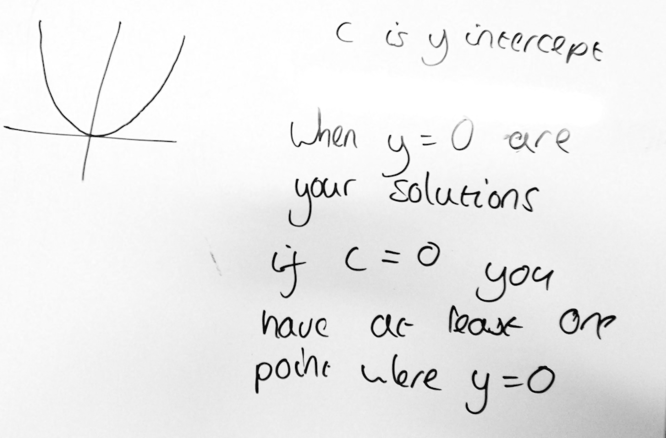
graphs with c=0

  • Try to explain the connection between graph and the written argument. How could you suggest the student makes this clearer?

  • What are the solutions of \(ax^2+bx+c=0\) if \(c=0\)?

Card 8

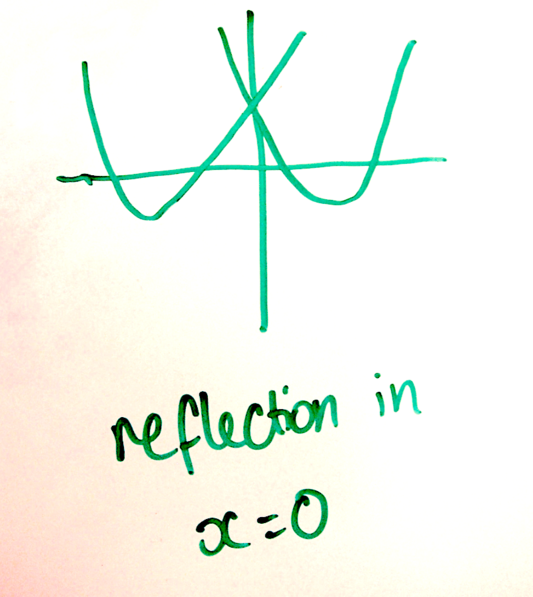
reflections of parabolas in y axis

  • Has this student considered a general example or a special case?

  • How could you use this idea to give a convincing argument for this card?

Card 9

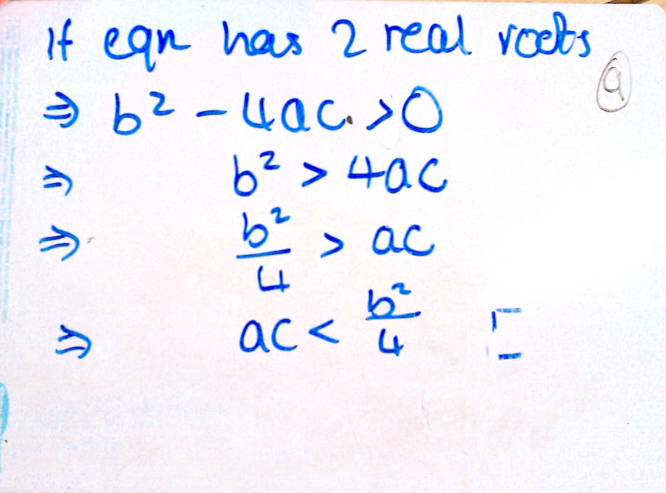
algebraic work
  • What other inequalities can you obtain from \(b^2-4ac>0\)?

Card 11

Two hand-drawn sets of axis. The first has 2 parabolas drawn where they both cross the x-axis at two points but the seocnd had a higher y-intercept and a steeper gradient. The second axis has a parabola and a straight line where the parabola crosses the x-axis twice and has a y-intercept of c=0 and the straight line has a positive gradient with a +c y-intercept

  • What do these examples show?

  • How could you modify the statement on card 11 so the two equations must have the same number of solutions?

Card 12

“Because they’ve all been turned to negatives, the \(b^2\) will still be a positive, but you times the \(-a\) and \(-c\) together to make a positive and times that by \(-4\) and then it’s a positive, minus negative times negative which makes negative.” Explanation by Student 1

Graph reflected in the x axis
Work by Student 2

  • What do you think student 1 and student 2 are trying to communicate?

  • What advice would you give them to help improve their solutions?

Previous Next
Last updated 18-May-17
Email Twitter
Terms Cookies Privacy
Rich resources for teaching A level mathematics
Copyright © and Database Right 2013-2025 University of Cambridge
All rights reserved
University of Cambridge logo
Department for Education logo