Can we find a quadratic inequality for each region of the Venn diagram?
The regions are defined as follows.
A: The solution set is a subset of \(x≤1\).
B: The solutions are given by \(a≤x≤b\) where \(a\) and \(b\) are real numbers.
C: The inequality is satisfied by \(x=4\), e.g. \(x=4\) satisfies the inequality \(x≥2\).
We will solve the given quadratic inequalities so they can be placed in the Venn diagram. We will start with the more straightforward ones.
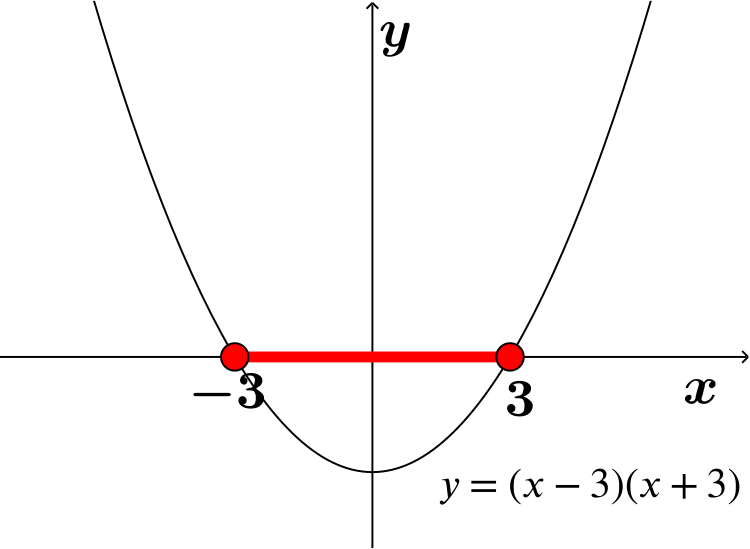
\(x^2≤9\)
|
\(x^2-9≤0\) \((x+3)(x-3)≤0\) From the graph we can see \(-3≤x≤3\) are the only real values of \(x\) that satisfy the inequality. Therefore, this inequality satisfies condition B only. |
|
\(11x≥2x^2\)
|
\(0≥2x^2-11x\) \(0≥x(2x-11)\) \(0≤x≤\frac{11}{2}\) This inequality satisfies conditions B and C. |

|
Does it matter whether we move the terms to the left or the right hand side of the inequality? What would change if we solved \(11x - 2x^2 ≥ 0\) instead?
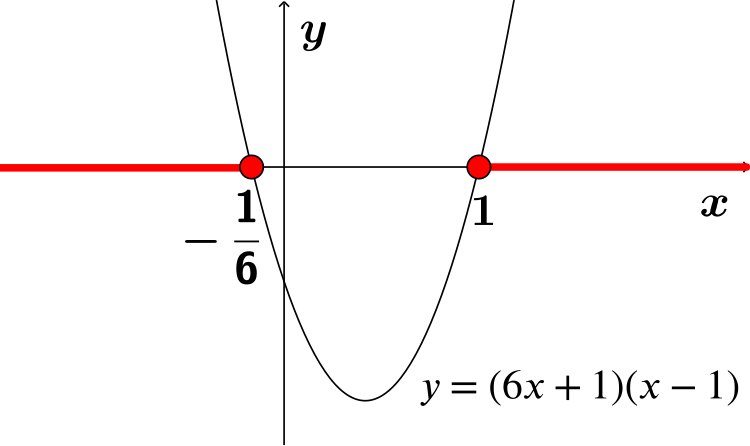
\(6x^2-1≥5x\)
|
\(6x^2-5x-1≥0\) \((6x+1)(x-1)≥0\) \(-\frac{1}{6}≤x\), \(x≥1\) This inequality satisfies condition C. |
|
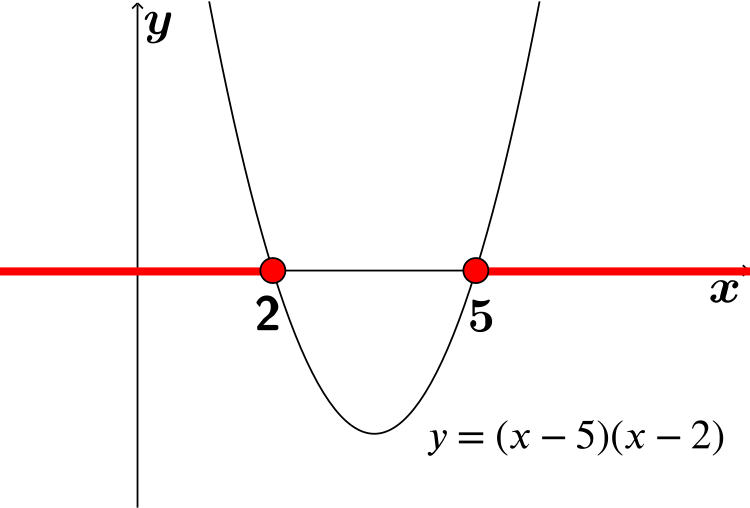
\(3x^2≥21x-30\)
|
Divide both sides of the inequality by \(3\) \(x^2≥7x-10\) \(x^2-7x+10≥0\) \((x-5)(x-2)≥0\) \(x≥5\), \(x≤2\) This inequality does not satisfy any of the conditions. |
|
Why can we divide both sides by \(3\)? How does the graph of \(y = 3x^2 - 21x + 30\) compare to the graph of \(y = x^2 - 7x +10\)?
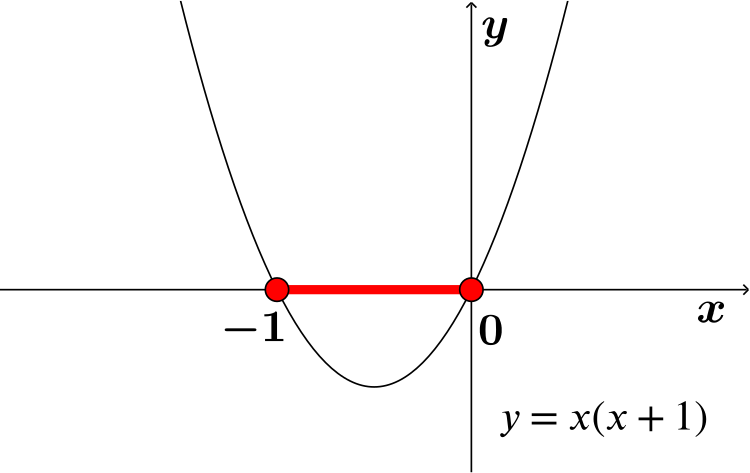
\(x^2≤-x\)
|
\(x^2+x≤0\) \(x(x+1)≤0\) \(-1≤x≤0\) This inequality satisfies conditions A and B. |
|
\(-2x^2≤x-6\)
|
\(0≤2x^2+x-6\) \(0≤(2x-3)(x+2)\) \(x≤-2\), \(x≥\frac{3}{2}\) This inequality satisfies C only. |
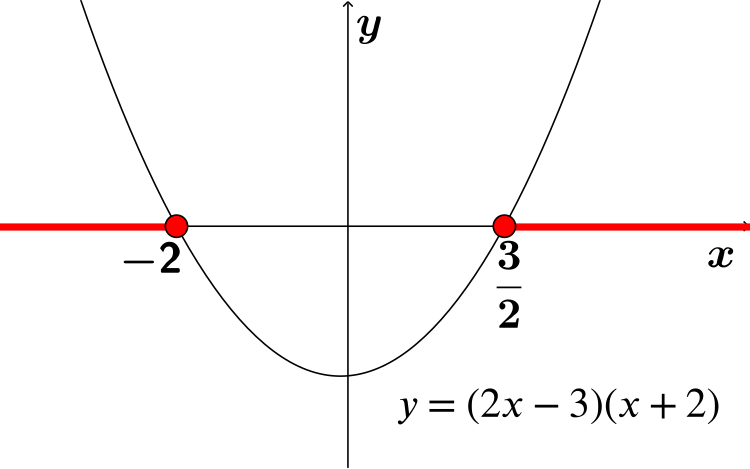
|
\(x^2+3≥2\)
|
\(x^2≥-1\) From the graph we can see that this inequality is true for all real values of \(x\). Therefore, this inequality satisfies C only. |

|
We didn’t try to solve this algebraically because of what we know about \(x^2\). What would happen if we did try to solve it algebraically?
\(x^2≤x-2\)
|
\(x^2-x+2≤0\) The discriminant of the quadratic \(x^2-x+2=0\) is \((-1)^2-4\times 1\times 2 = -7\). This means there are no real solutions to the quadratic equation and therefore no real solutions to the quadratic inequality. This can be seen from the graph. For all real values of \(x\), it is impossible for the graph \(y=x-2\) to be greater than the graph \(y=x^2\). Therefore, this inequality does not satisfy any of the conditions. |
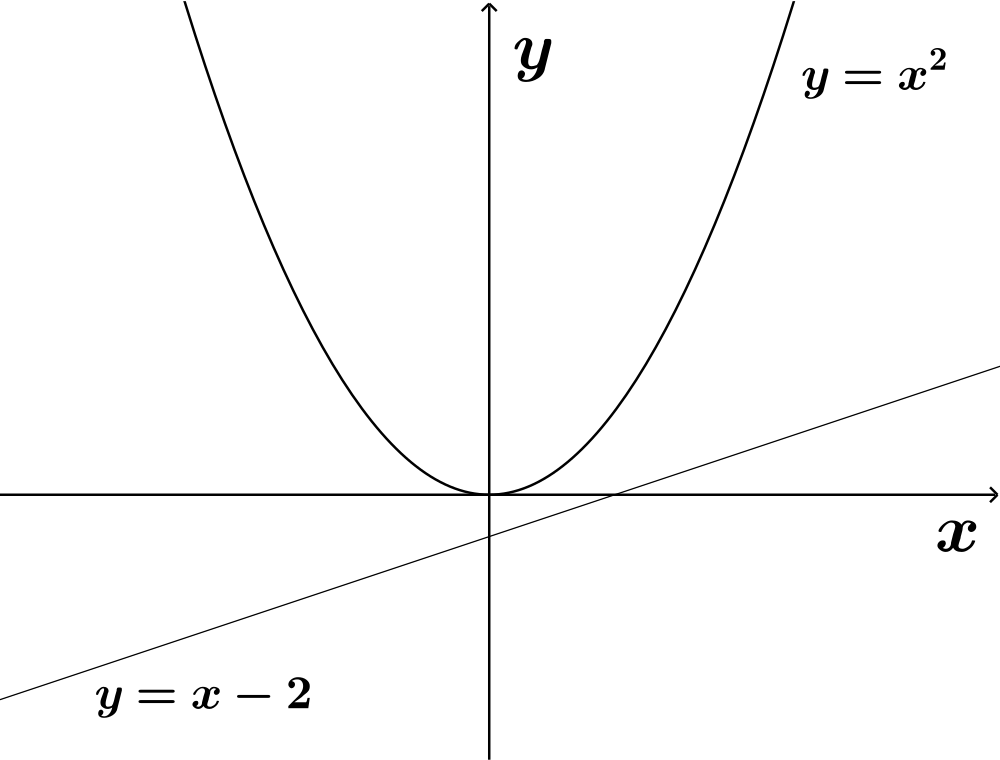
|
What other graph might we have sketched to see there are no solutions?
Here are the given inequalities presented in the Venn Diagram.


