What’s the same and what’s different about the following pairs of equations?
\(y=x^2-4\) and \(y+x^2-4=0\)
Let’s consider the first pair. Rearranging the second equation gives \(y=-x^2+4\). The difference between this and the first equation is that the signs are reversed on the right-hand side.
Both equations are quadratic and therefore represent parabolas when plotted on a coordinate grid. Thinking about the properties of the parabolas we can immediately see that the \(y\)-intercepts are at \(y=4\) and \(y=-4\) and that the first has a positive coefficient of \(x^2\) and the second has a negative coefficient of \(x^2\) so will be an ‘upside down’ parabola.
If we factorise both equations then we can find their roots. Factorising the first equation gives \(y=x^2-4=(x+2)(x-2)\) so it has roots at \(x= \pm 2\). Similarly, the second equation \(y=-x^2+4=-(x+2)(x-2)\). It also has its roots at \(x=2\) and \(x=-2\).
We have factorised the difference of two squares.
So the combined image of the two parabolas is symmetrical about both the \(x\) and \(y\)-axes.
To summarise, the two equations both represent parabolas that have the same roots. The equations represent two different parabolas as the coefficient of \(x^2\) and the \(y\)-intercept both differ.
\(y=4-9x^2\) and \(y+4=9x^2\)
If we now consider the second pair of equations we find a similar result. Rearranging the second equation gives \(y=9x^2-4\) which is the first equation with the signs reversed on the right-hand side.
Both equations are quadratic and can be represented as parabolas with a \(y\)-intercept at \(y=4\) and \(y=-4\) respectively. Factorising both equations gives \(y=4-9x^2=(2+3x)(2-3x)\) and \(y=9x^2-4=(3x+2)(3x-2)\). We can see that the (common) roots of both equations are at \(x=-\frac{2}{3}\) and \(x=\frac{2}{3}\).
The combined image of the two parabolas is once again symmetrical about both the \(x\) and \(y\)-axes.
To summarise, the two equations both represent parabolas that have the same roots. The equations represent two different parabolas as the coefficient of \(x^2\) and the \(y\)-intercept both differ.
\(2y=4x^2-6\) and \(-(y-3)=2x^2\)
Finally we shall consider the third pair of equations. Rearranging the first gives \(y=2x^2-3\) and the second \(y=-2x^2+3\).
Both equations are quadratic and can be represented as parabolas with a \(y\)-intercept at \(y=3\) and \(y=-3\) respectively.
Factorising both equations gives \[y=2x^2-3=(\sqrt{2}x+\sqrt{3})(\sqrt{2}x-\sqrt{3})\] and \[y=-2x^2+3=(-\sqrt{2}x+\sqrt{3})(\sqrt{2}x+\sqrt{3}).\]
We can see that the (common) roots of both equations are at \(x=-\frac{\sqrt{3}}{\sqrt{2}}\) and \(x=\frac{\sqrt{3}}{\sqrt{2}}\).
The combined image of the two parabolas is once again symmetrical about both the \(x\) and \(y\)-axes. To summarise, the two equations both represent parabolas that have the same roots. The equations represent two different parabolas as the coefficient of \(x^2\) and the \(y\)-intercept both differ.
All three pairs of equations share the property that they are quadratic and, when represented graphically, each pair of equations produces a pair of parabolas. The combined image of each pair is symmetrical about the \(x\) and \(y\)-axes. Each equation is distinct because of differences in the coefficients of \(x^2\) and the values of the \(y\)-intercept.
If you were given the following picture, could you suggest the equation of its pair?
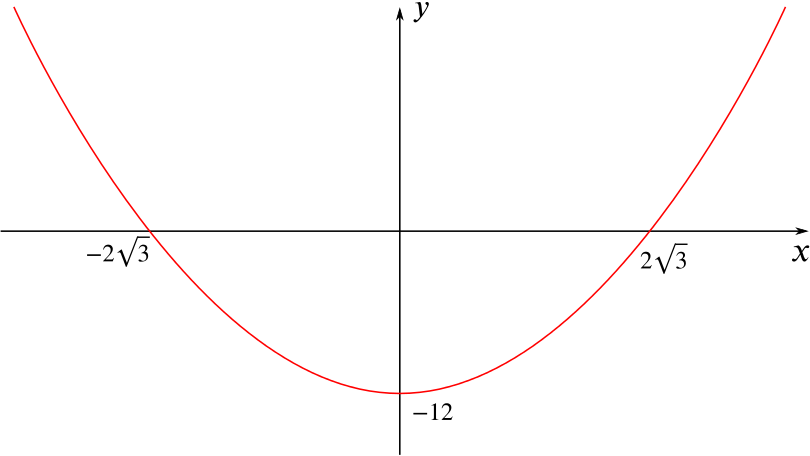
From the diagram we can see that the parabola has roots at \(\pm 2\sqrt{3}\). From the shape of the parabola we can see that the coefficient of \(x^2\) will be positive.
So far this gives us that \(y=a(x+\sqrt{12})(x-\sqrt{12})\) where \(a>0\). Expanding the brackets and simplifying this expression gives \(y=ax^2-12a\). From the diagram we know that the \(y\)-intercept is at \(y=-12\). Substituting into our equation shows that when \(x=0\), \(y=-12a\), so we deduce that \(a=1\).
We have expanded the difference of two squares.
Now that we know the equation of the parabola in the diagram we can find its pair. We know that it will have the same roots but a \(y\)-intercept at \(y=12\) to create symmetry in the \(x\)-axis. This means that \(a=-1\) in the equation above, giving \(y=-x^2+12\).
How about if you were given this picture instead? Could you give the equation of its pair?
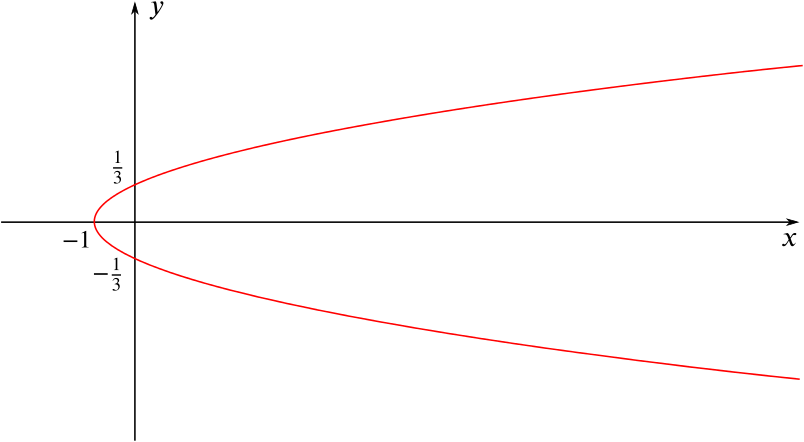
This picture shows another parabola but instead with the \(x\)-axis is its line of symmetry.
This suggests that the equation is of the form \(x=ay^2+by+c\). It would seem logical to treat this problem in exactly the same way as that above. We can see roots at \(y=\pm \frac{1}{3}\) and this suggests an equation of the form \(x=a\left(y+\frac{1}{3}\right)\left(y-\frac{1}{3}\right)\).
From the graph we can see that the \(x\)-intercept is at \(x=-1\). In order to achieve this we need \(a=9\) so that the equation is \(x=(3y+1)(3y-1)=9y^2-1\).
Now to find its pair. We know that it will have the same roots but an \(x\)-intercept at \(x=1\). Therefore the paired parabola will be given by the equation \(x=-(3y+1)(3y-1)=1-9y^2\).

