Sort these quadratic equations into groups.
- How will you choose to define the groups?
- Are there some equations which belong to more than one group?
Once you have sorted the equations into groups, write a further equation for each group.
How else could you have sorted the equations?
Here is one possible way to group the equations. We ended up using seven groups. We felt that some of the equations fitted into more than one group, so we’ve drawn it like that.
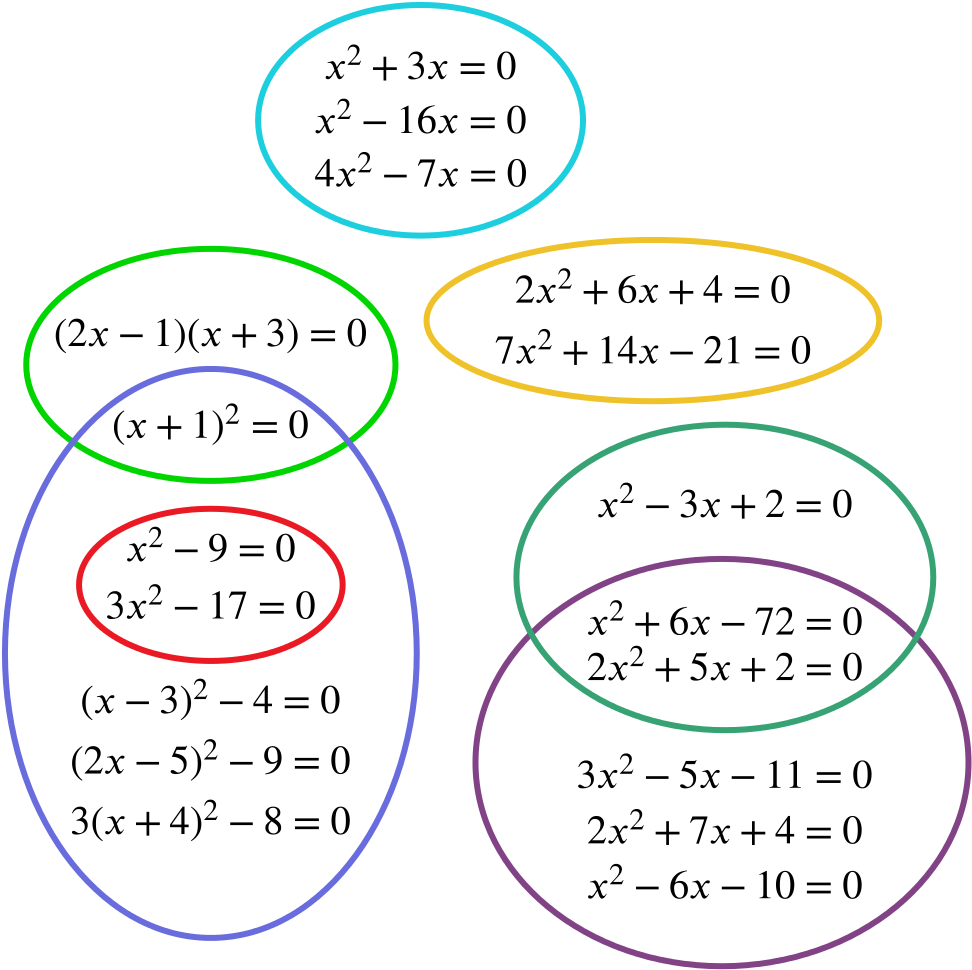
What rules might we have used for our groups?
How does our grouping compare with yours?
Which equations can only be solved in the way we’ve stated?
Which equations could reasonably be solved in other ways?
Are there any equations that could be solved in other ways, but it wouldn’t make sense to do so?
Are there some equations which you would solve in one way if you had a calculator, but in a different way if you did not?
Do you actually need to solve the equations in order to sort them?

