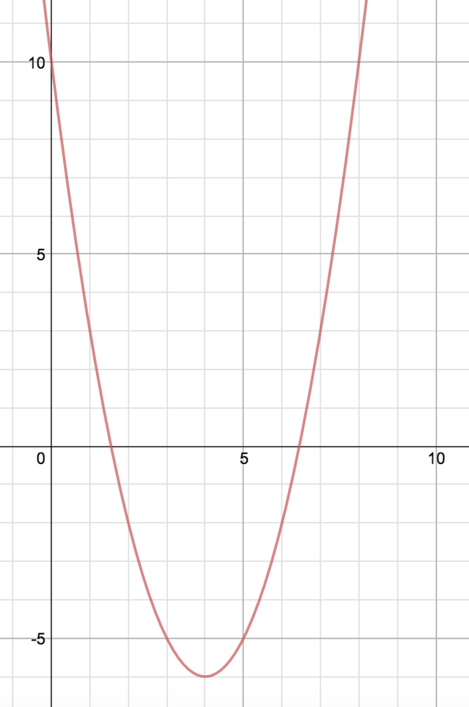
The equation of this graph is \(y = x^2 - 8x + 10\)
Is this graph symmetrical? Are you convinced? How can you convince someone else?
Approach 1
It looks like the graph has a line of symmetry with equation \(x = 4\).
If we can show that each point on the curve has a mirror image about the line \(x=4\), then we will be correct.
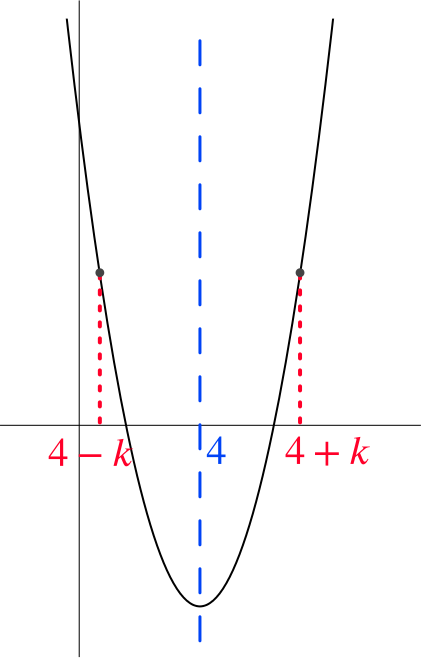
Let’s choose \(x\) coordinates such that they are equidistant from the line \(x=4\), e.g. \(x=4+k\) and \(x=4-k\).
When \(x = 4 + k\), \(\quad y = (4 + k)^2 - 8(4 + k) + 10 = k^2 - 6\).
When \(x = 4 - k\), \(\quad y = (4 - k)^2 - 8(4 - k) + 10 = k^2 - 6\).
The \(y\) coordinates are equal. This shows we are correct and the graph \(y = x^2 - 8x + 10\) is symmetrical about the line \(x = 4\).
Alternatively, we can perform the same calculation with the completed square form. What do you notice?
What did we do in this approach? We made a conjecture (an educated guess) and then went on to prove that this was correct. This is a fundamental process in doing mathematics.
Approach 2
It looks like the graph of \(y = x^2 - 8x + 10\) has the same shape as \(y = x^2\) but is in a different position.
If we can show that \(y = x^2\) is symmetrical and we can translate the graph \(y = x^2\) to \(y = x^2 - 8x + 10\), then we have shown that \(y = x^2 - 8x + 10\) is symmetrical. We do this in two steps.
Step 1: Show that the graph \(y = x^2\) is symmetrical about the \(y\) axis.
When \(x = k\), \(\quad \phantom{-}y = k^2\).
When \(x = -k\), \(\quad y = k^2\).
By a similar argument to Approach 1 above, the graph of \(y = x^2\) is symmetrical about the \(y\) axis.
Note: A function where \(f(x) = f(-x)\) for all \(x\) is called an even function and is symmetrical about the \(y\) axis. There is more on this topic in Odd or even or ….
Step 2: Rewrite \(y = x^2 - 8x + 10\) as a translation of \(y = x^2\).
By completing the square, we have \(y=x^2 - 8x + 10 = (x - 4)^2 - 6\) which is a translation of the graph \(y = x^2\) by \(\dbinom{4}{-6}\). The line of symmetry is therefore translated to \(x = 4\) and the vertex is translated to (\(4,-6\)).
Therefore the graph \(y = x^2 - 8x + 10\) is symmetrical.
How do these approaches compare?
Which is the more easily generalised?
How would these approaches help us to consider whether all quadratics are symmmetrical?

