When is $12x^2+7x-10$ negative?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

This is the same as asking: when is the curve \(y = 12x^2+7x-10\) below the \(x\)-axis?

Let’s start by finding when \(y = 0\). We can use the quadratic formula here, giving the roots as \[\frac{-7 \pm \sqrt{49 + 480}}{24} = -\dfrac{5}{4}\ \text{and}\ \dfrac{2}{3}.\]

(We could factorise here, but the factorisation \((3x-2)(4x+5)\) could take us a while to spot.)

The coefficient of \(x^2\) is positive here, so the curve is ‘vertex-down’. We have enough information now to sketch the curve.

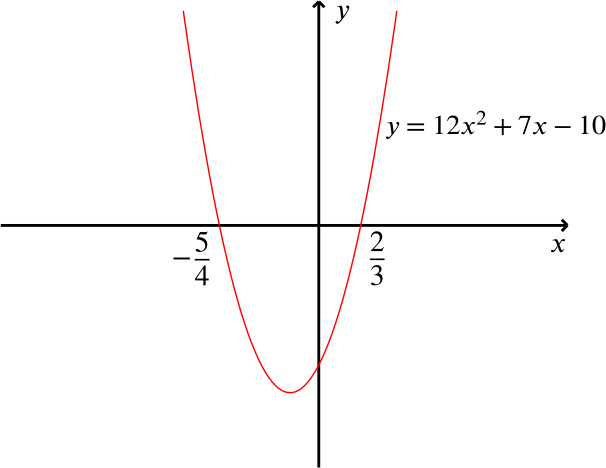
So the expression \(12x^2+7x-10\) is negative for \(-\dfrac{5}{4}<x<\dfrac{2}{3}\).

We note that since the coefficient of \(x^2\) is positive, \(x^2+4x+c\) will always be positive for some values of \(x\), and the curve \(y=x^2+4x+c\) is ‘vertex-down’.

So the question is the same as asking: which values of \(c\) mean that the curve \(y = x^2+4x+c\) is always above the \(x\)-axis?

This means there are no roots for \(y = 0\), and so the discriminant must be negative.

So we have \(4^2-4c < 0\), or \(c > 4\).

Hence the expression is always positive if and only if \(c > 4\).