Consider the equation \[x^2-bx+c=0,\] where \(b\) and \(c\) are real numbers.
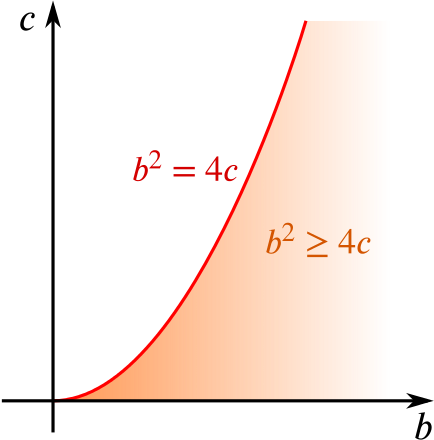
- Show that the roots of the equation are real and positive if and only if \(b>0\) and \(b^2\geq 4c>0\), and sketch the region of the \(b\)-\(c\) plane in which these conditions hold.
We need to show an ‘if and only if’ statement, so let’s consider the two directions separately to make sure that we get the logic straight.
Approach 1
First suppose that the roots of the equation \[\begin{equation} x^2-bx+c=0 \label{eq:1} \end{equation}\]are real and positive. From the quadratic formula, we see that the roots of \(\eqref{eq:1}\) are of the form \[\frac{b\pm\sqrt{b^2-4c}}{2}.\] For the root or roots to be real, we require that \(b^2-4c \geq 0\), that is, \(b^2 \geq 4c\). In order for them to be positive, we require that \[b-\sqrt{b^2-4c}>0.\] This immediately tells us that \(b > 0\), but we can go further. We can rearrange this to get \[b > \sqrt{b^2-4c},\] which (assuming that \(b>0\)) is true if and only if \[b^2 > b^2-4c,\] since both sides of the inequality are positive so we may square. But then \[4c > 0.\] That is, if the roots are real and positive then \(b>0\) and \(b^2 \geq 4c>0\).
Now suppose that \(b>0\) and \(b^2 \geq 4c>0\).
Then the roots of \(\eqref{eq:1}\) are real since \(b^2-4c\geq 0\), and \(b>0\) guarantees that the root \(b + \sqrt{b^2 - 4c}\) is positive.
So it remains to show that \(b-\sqrt{b^2-4c}>0\). We have that \[4c>0,\] so that \[b^2>b^2-4c,\] then square rooting shows that \[b>\sqrt{b^2-4c},\] so the roots of \(\eqref{eq:1}\) are real and positive, as required.
Approach 2
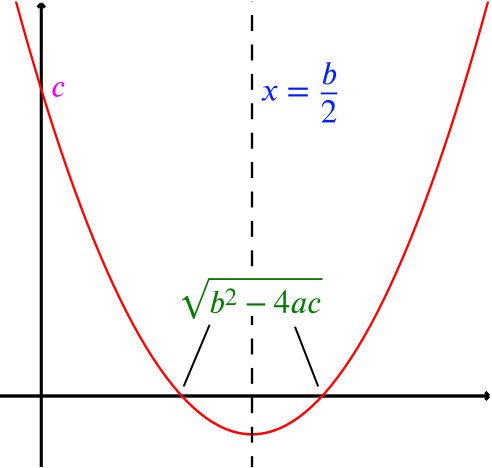
This is intended to be a proof without words! We have from the diagram that:
If \(c\), \(b\) and \(b^2-4c\) are all positive, there are two real positive roots for \(x^2 -bx +c = 0\) (if \(b^2 = 4c\), we have two real positive equal roots).
If there are two real positive roots for \(x^2 -bx +c = 0\), then \(c\) and \(b\) are positive and \(b^2-4c\) is non-negative.
(Why is the distance between the roots \(\sqrt{b^2-4c}\)?)
Approach 3
When solving problems about the roots of polynomials, it is often useful to find expressions those roots must satisfy and see if this tells us anything new. If \(\alpha\) and \(\beta\) denote the roots of the equation, then
\[x^2-bx+c=(x-\alpha)(x-\beta)=x^2-(\alpha+\beta)x+\alpha\beta\]
and so \(\alpha + \beta = b\) and \(\alpha \beta = c\).
We also know that the roots of a quadratic equation are real if and only if the discriminant is non-negative, that is, if and only if \(b^2-4c \geq 0\).
Using these facts, if \(\alpha\) and \(\beta\) are both real and positive, then \(b = \alpha + \beta >0\), \(c=\alpha \beta >0\) and \(b^2 \geq 4c\), as above.
Conversely, if \(b>0\) and \(b^2 \geq 4c > 0\), then we know the discriminant is positive and hence both roots are real. We also have that \[\begin{equation} \alpha \beta > 0 \label{eq:2} \end{equation}\] and \[\begin{equation} \alpha + \beta > 0. \label{eq:3} \end{equation}\]As \(\alpha\) and \(\beta\) are both real, by \(\eqref{eq:2}\), we know that \(\alpha\) and \(\beta\) are either both positive or both negative. However, if \(\alpha\) and \(\beta\) were both negative, then \(\eqref{eq:3}\) could not possibly hold. Hence \(\alpha\) and \(\beta\) are both positive, as required.
We now sketch on a graph the region where \(b>0\), \(c>0\) and \(b^2\geq 4c\):
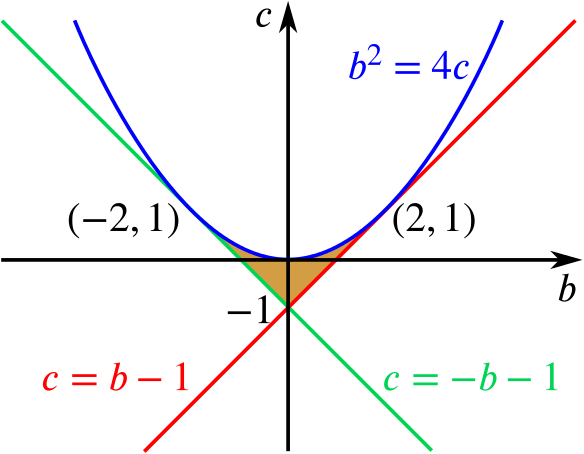
- Sketch the region of the \(b\)-\(c\) plane in which the roots of the equation are real and less than \(1\) in magnitude.
We have \(\dfrac{b-\sqrt{b^2-4c}}{2} \leq \dfrac{b+\sqrt{b^2-4c}}{2}\) so we only need to consider the values for which both \[ -1 < \frac{b-\sqrt{b^2-4c}}{2} \quad \text{and} \quad \frac{b+\sqrt{b^2-4c}}{2} < 1.\]
Firstly, we will consider the values for which \[b+\sqrt{b^2-4c}<2.\] Rearranging gives \[\sqrt{b^2-4c}<2-b.\] So \(b < 2\), as the square root is non-negative, and we can square both sides to get \[b^2-4c<4-4b+b^2,\] which we may rearrange to find \(c>b-1\).
We will now consider the values for which \[-2 < b -\sqrt{b^2-4c}.\] Similarly, we can rearrange to get \[\sqrt{b^2-4c} < b+2.\] So \(b > -2\), and we can, as before, square to get \[b^2-4c < b^2+4b+4,\] and hence \(c>-b-1\).
To sketch the graph, we start by considering the boundary curves \(b^2 =4c\), \(c=b-1\) and \(c=-b-1\), and the points at which they intersect. We can see that the two lines only intersect when \(b=0\) and \(c=-1\), and the lines intersect the curve when
\[b^2 = 4b -4 \quad \text{and} \quad b^2= -4b -4\] which rearrange to \[(b-2)^2=0 \quad \text{and} \quad (b+2)^2=0.\]
This tells us that each line intersects with the curve in only one place and so these lines must be tangent.
Is there a way we could have deduced this directly from \(\eqref{eq:4}\)?
What do the lines being tangent signify in terms of our equation \(x^2-bx+c=0\)?
Is this a representation of a well-known property of these equations?
Sketching the graph then yields the following picture:
We might notice that when we derived the inequalities \(c>b-1\) and \(c>-b-1\), a lot of the work we did was very similar.
We might also notice that the graph above is symmetric about the \(c\) axis. Why is this?
Does the graph give us any ideas about how we might deduce one inequality from the other?

