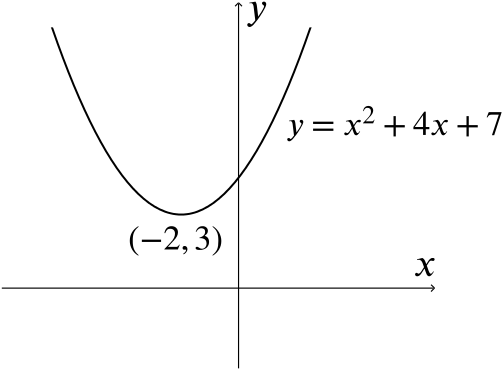The least value of the function \(x^2+px+q\) is \(3\), and this occurs when \(x=-2\). Find the values of \(p\) and \(q\).
By completing the square, we can express any quadratic polynomial in the form \(a(x-r)^2+s\) for some \(a\), \(r\) and \(s\).
From this, if \(a\) is positive, the least value is \(s\), and this occurs when \(x=r\).
For our question, we must have that \[x^2+px+q = (x+2)^2+3 = x^2+4x+7,\] and so, by comparing coefficients, we get \(p=4\) and \(q=7\). A sketch of the curve can be seen below.