When does $x^2+(3k-7)x+(2k+6)=0$ have real roots?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

A quadratic equation \(ax^2 + bx + c = 0\) has real roots if and only if its discriminant \(b^2-4ac \geq 0\).

Substituting in the quadratic’s coefficients, we find that for real roots here, we must have \[\begin{align*} &&(3k-7)^2 -4(2k+6) &\geq 0 &&\quad\\ \iff\quad&& 9k^2 -42k + 49 -8k -24 &\geq 0 \\ \iff\quad&& 9k^2 -50k + 25 &\geq 0 \\ \iff\quad&& (9k-5)(k-5) &\geq 0. \end{align*}\]

The solutions of the quadratic equation \((9k-5)(k-5)=0\) are \(k=\frac{5}{9}\) and \(k=5\), so we can sketch the graph of \(y=(9k-5)(k-5)\):

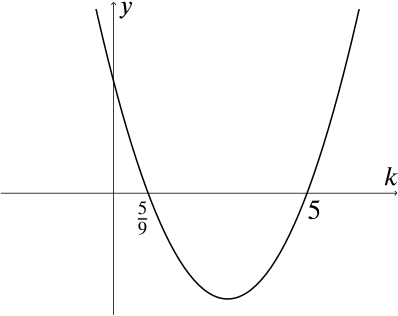
Therefore, the equation has real roots when \(y\ge0\), which is when \(k\geq 5\) or \(k \leq \dfrac{5}{9}\).