Rearranging the second equation, we find that \[y^2=\frac{7x^2+17}{5}.\]
Substituting this in to the first equation gives \[3x^2-13xy+9\left(\frac{7x^2+17}{5}\right)=15.\]
Making \(y\) the subject here gives \(y = \dfrac{6x^2+6}{5x}\).
Now substituting this into the second equation gives
\[7x^2-5\left(\frac{6x^2+6}{5x}\right)^2+17=0,\]
which simplifies to
\[x^4-13x^2+36=0.\] This is a quadratic in \(x^2\) that we can factorise: \[x^4-13x^2+36=(x^2-9)(x^2-4)=0.\] So we deduce that \(x=\pm2\) or \(x=\pm3\).
To find \(y\), we can return to \(y = \dfrac{6x^2+6}{5x}\).
This gives us the four solutions \((x,y)=(2,3)\), \((-2,-3)\), \((3,4)\), and \((-3,-4)\).
We can then check that each of these pairs does, indeed, satisfy both equations.
We might notice that both of the starting equations are of degree 2 in \(x\) and \(y\). Graphically, each of these represents a conic, that is, a circle, an ellipse, a parabola or a hyperbola. (There are also some degenerate possibilities, which we will not consider here.)
In this case, both equations give hyperbolas.
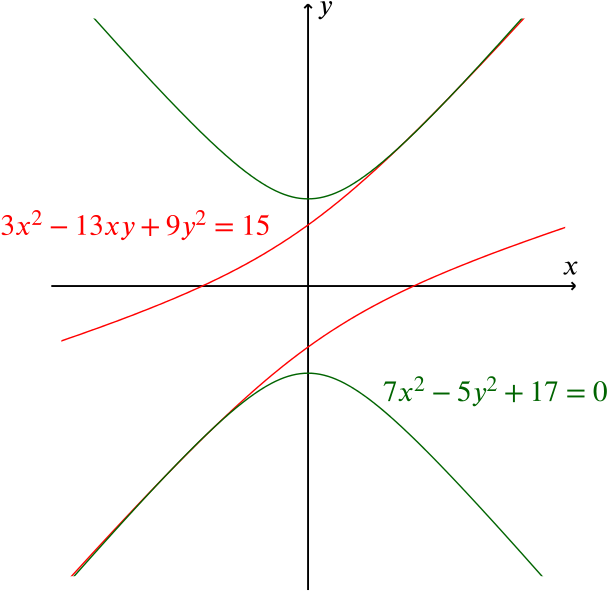
Two conics intersect in at most four points (as here), although there may be fewer crossing points (two circles may not intersect at all, for example). This is an example of Bézout’s Theorem.

