Into how many regions is the plane divided when the following three parabolas are drawn?
\[y = x^2\] \[y = x^2 - 2x\] \[y = x^2 + 2x +2.\]
\(4\),
\(5\),
\(6\),
\(7\).
One approach is to sketch the three parabolas. We could write their equations (by completing the square) as
\[y = x^2\] \[y = (x-1)^2 - 1\] \[y = (x+1)^2 + 1.\]
So we could describe all three as ‘vertex-down’ parabolas, with their vertices at \((0,0)\), \((1,-1)\) and \((-1,1)\) respectively.
To help us with our sketch, their \(y\)-intercepts are \(0\), \(0\) and \(2\) respectively.
To get from the first curve to the second, we translate \(y = x^2\) right \(1\) and down \(1\).
To get from the first curve to the third, we translate \(y = x^2\) left \(1\) and up \(1\).
So they are congruent copies of each other, with parallel axes of symmetry.
It should be intuitively clear from this that each pair of parabolas will meet in exactly one point.
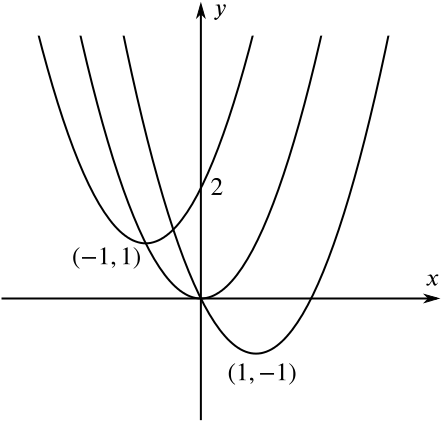
From the graph, we can see that there are seven regions, so the answer is (d).
Alternatively, we can solve the equations two at a time. We have
\[y = x^2, \hspace{3mm} y = x^2 - 2x \hspace{3mm} \Longrightarrow \hspace{3mm} x = 0\]\[y = x^2, \hspace{3mm} y = x^2 + 2x +2 \hspace{3mm} \Longrightarrow \hspace{3mm} x = -1\]\[y = x^2 - 2x, \hspace{3mm} y = x^2 + 2x +2 \hspace{3mm} \Longrightarrow \hspace{3mm} x = -\frac{1}{2}\]
This confirms algebraically that each pair of parabolas intersects exactly once.
How many regions do we have? Let’s count them. The first parabola splits the plane into two regions.
Then the second parabola intersects the first parabola once, and so splits the two regions into two, leaving four regions.
Finally, the third parabola crosses each of the other two parabolas once, and so passes through three of the four regions, splitting each of these into two.
So there are now seven regions altogether.
Interestingly, the question of the number of regions formed will be unaffected if we add the same function to each of the three given functions.
For example, if we added \(x^3\) to each of them, each of the graphs would be distorted, but in exactly the same way (vertically speaking), and so the number of regions would be unchanged.
So if we subtract \(x^2\) from each of the equations, we are left with the three straight lines: \[\begin{align*} y &= 0\\ y &= -2x\\ y &= 2x + 2. \end{align*}\]These straight lines are not parallel, and are not concurrent, so we can sketch (any) three lines and observe that they divide the plane up into seven regions.

