The values of \(k\) for which the line \(y=kx\) intersects the parabola \(y=(x-1)^2\) are precisely
\(k\le0\),
\(k\ge-4\),
\(k\ge0 \hspace{2mm} \textrm{or} \hspace{2mm} k\le-4\),
\(-4\le k\le0\).
The line \(y=kx\) intersects the parabola \(y=(x-1)^2\) when the equation
\[(x-1)^2 = kx\]
has real solutions.
Rearranging this equation gives
\[x^2 - (k+2)x + 1 =0,\]
which has discriminant \((k+2)^2-4\).
For the quadratic to have real solutions we need the discriminant to be non-negative, that is \((k+2)^2 \geq 4\), so we need either
\[\begin{align*} k+2 &\ge 2 \\ \textrm{or}\quad k+2 &\le -2, \end{align*}\]i.e., \(k \ge 0\) or \(k \le -4\).
So the answer is (c).
Alternatively a sketch shows us what is happening.
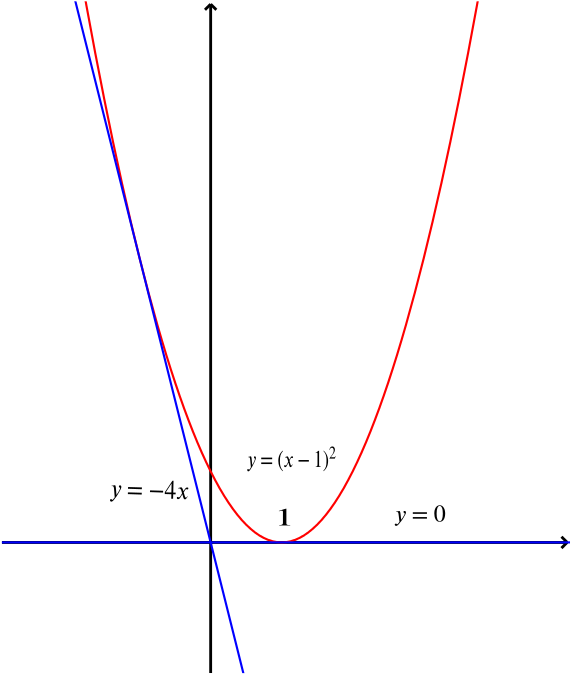
It’s clear from the sketch that any line with positive gradient cuts the parabola, and that \(y = -0.01x\) certainly does not. So the only possible option is (c).

