Take a look at the graph below.
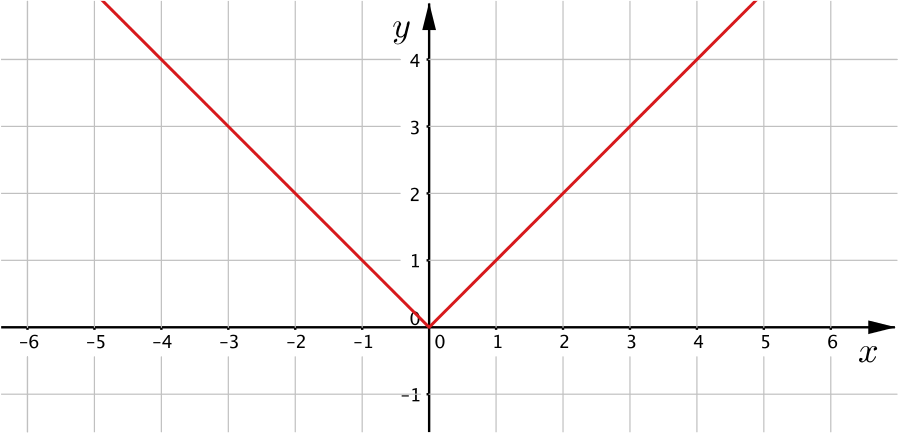
How would you describe it?
What questions might you ask yourself about this graph?
Is this a proper function?
Does it matter that it has two different parts?
Is there a formula for this?
Broadly speaking, a function gives a single output for each input. If you choose any \(x\)-value and use the graph to give you the corresponding \(y\)-value, you will get only one \(y\)-value, so this graph does represent a function.
It is important not to confuse the fact that every \(x\)-value has a single \(y\)-value with the fact that there may be more than one value of \(x\) that gives the same value of \(y\).
The two different parts of the graph don’t stop it being a function, but they do mean that we may need a different rule for different inputs. In the case of this graph, for positive values of \(x\) and \(0\) the graph is \(y=x,\) i.e. the output is equal to the input. For negative values of \(x,\) the graph is \(y=-x,\) i.e. the function multiplies the input by \(-1\). These rules cover all possibilities for input values, so our function is the rule \[f(x)=x \,\,\text{if } x \geq 0 \,\, \text{and } f(x)=-x \,\, \text{if } x<0.\] This is sometimes written more compactly as \(f(x) = \begin{cases}x & \text{if } x \geq 0 \\ -x & \text{if } x <0. \end{cases}\)
We could have attached \(f(0)=0\) to the left-hand section of the graph instead, but the convention is to include it in the right-hand section.
This function is known as the modulus function. It is often written as \(\vert x \vert\) and pronounced ‘mod \(x\)’. It is also called the absolute value function. It is worth noting that the name ‘modulus function’ is not universal and modulus has several different meanings in mathematics.
Are there other functions that look similar to this?
How could I move the ‘corner’?
What would the function \(f(x)=\vert x-2\vert\) look like? What about \(f(x)= \vert 3x\vert\)?
The sections of the original graph meet at \(x=0\), which is why there appears to be a ‘corner’ at \((0,0)\). What would happen if the sections met somewhere else? What similar functions would have sections meeting at \((3,0)\) or at \((-2,0)\)? What about sections meeting at \((3,5)\)?
The original function is symmetric about the \(y\)-axis. Can you define a function like this which doesn’t have a vertical line of symmetry?
The original function doesn’t output any negative values, but can you define a function like this that does output negative values?
How would a function like this occur?
How could it be used?
What could a function like this model?
What is the difference between \(3\) and \(5\)? What about \(5\) and \(3\)? In some situations, you might not be interested in which number is bigger, but in the size of the gap between them. For example, if you are trying to solve an equation using trial and improvement, you might decide to stop once successive answers are closer together than \(0.01\).
If a car is driving at constant speed past you, the graph of the distance of the car from you, plotted against time, would look like the graph of a modulus function.
The amount of force in a stretched or compressed spring is proportional to how much the spring has been compressed or extended, i.e. the modulus of the difference between the original and new lengths.

