The following five functions have been plotted accurately on the axes below.
\(y=\sqrt{x}\)
\(y=x^2\)
\(y=x\)
\(y=\dfrac{x^2+x}{2}\)
\(y=2\sqrt{x}-x\)
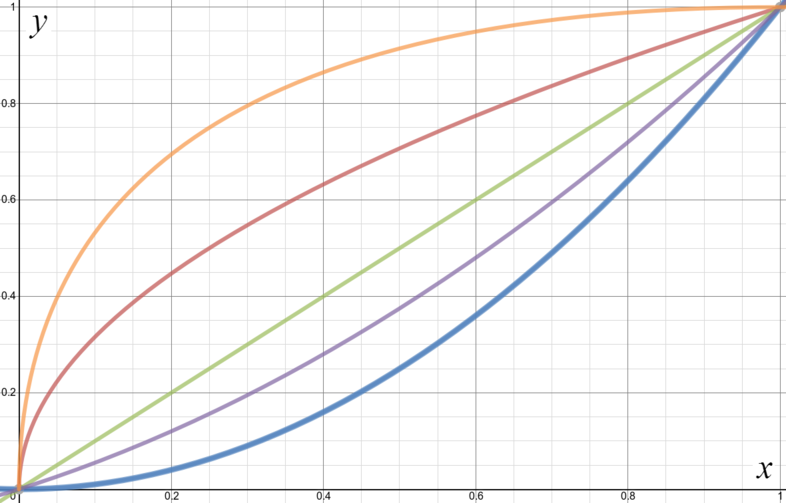
Can you label each curve?
We know that \(y = x\) is a straight line, passing through both the origin and \((1,1)\), so this is the middle ‘curve’.
For \(x\) between \(0\) and \(1\), we know that \(x^2 < x\), so the curve \(y = x^2\) must lie below the straight line. Similarly, for these \(x\) we have \(\sqrt{x} > x\) and so the curve \(y = \sqrt{x}\) lies above the straight line.
Now \(y = \dfrac{x^2 + x}{2}\) is the average of \(x^2\) and \(x\), so must lie between the two. So working down from \(y = x\) (the straight line in the middle) we first reach \(y = \dfrac{x^2 + x}{2}\) and then \(y = x^2\).
Since \(\sqrt{x} > x\), we have \(2\sqrt{x} - x > \sqrt{x}\). So working up from \(y = x\) we first reach \(y = \sqrt{x}\) and then \(y = 2\sqrt{x} - x.\)
To summarise, from top to bottom we have \(y = 2\sqrt{x} - x\), then \(y = \sqrt{x}\), then \(y = x\), then \(y = \dfrac{x^2 + x}{2}\), and finally \(y = x^2\) at the bottom.
Imagine that you wish to plot a route between \((0,0)\) and \((1,1)\). Can you find a function that does this without intersecting any of the existing curves, except at the end points?
What other curves can you plot that intersect the existing curves only at the end points?
There are many curves that we could choose.
One way to generate many examples would be to take averages of two or more of the above curves, in just the same way that we took the average of \(x\) and \(x^2\) to get a new curve. We might need to be a bit careful in our choice of curves in order to ensure that the new curve does not intersect any of the existing curves other than at the end points.
We could pick a polynomial such as \(y = x^3\); we can check that this intersects the existing curves only at \(x = 0\) and \(x = 1\).

