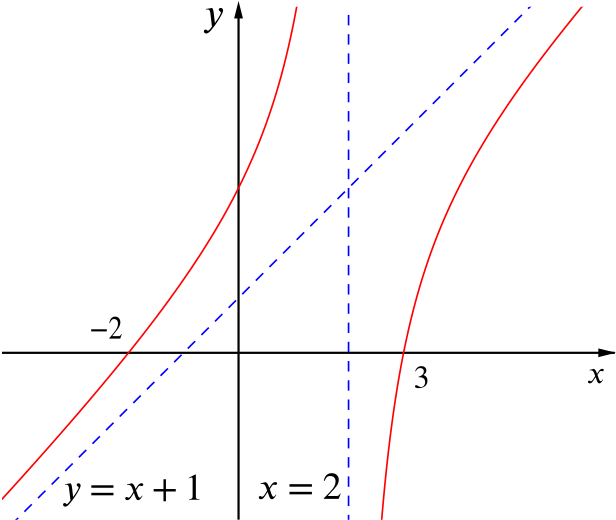
Write down the equations of the two asymptotes of the curve \[y = x+ 1 - \frac{4}{x-2}\] and find the coordinates of the points at which the curve meets the axes.
Sketch the curve.
When \(x=2\), the denominator is zero, so there is a vertical asymptote at \(x=2.\)
If we look at what happens on either side of \(x=2\), we see that \(\dfrac{4}{x-2}\) gets very large and positive as \(x\) approaches \(2\) from the left, and \(\dfrac{4}{x-2}\) gets very large and negative as \(x\) approaches \(2\) from the right.
As \(x\) tends to infinity in either the positive or negative direction, the term \(-\dfrac{4}{x-2}\) tends to \(0\), so the graph of \(y= x+ 1 - \dfrac{4}{x-2}\) approaches the line \(y=x+1\). Therefore \(y=x+1\) is the other asymptote.
Setting \(x = 0\) gives \(y = 3\), so the curve meets the \(y\)-axis at 3.
Setting \(y = 0\) gives \(x + 1 - \dfrac{4}{x-2} = 0\), which yields a quadratic equation. \[\begin{align*} & x + 1 - \frac{4}{x-2} = 0 \\ \iff & (x+1)(x-2) = 4 \\ \iff & x^2 - x - 6 = 0 \\ \iff & (x+2)(x-3) = 0 \\ \iff & x = 3 \textrm { or } x = -2. \end{align*}\]So the curve meets the \(x\)-axis at \(-2\) and \(3\). We can now deduce the shape of the graph.