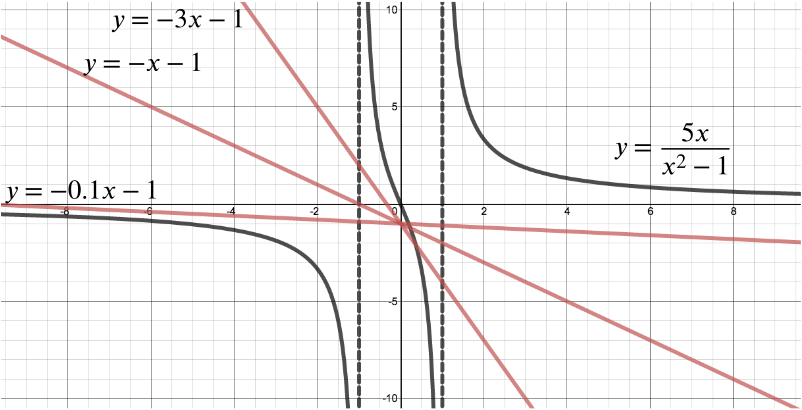
Sketch the graph of \[y = \dfrac{5x}{x^2 -1},\] showing clearly the three asymptotes.
Vertical asymptotes
The vertical asymptotes occur where the denomiator is \(0\).
We can factorise the denominator of \(y = \dfrac{5x}{x^2 - 1}\) to get \[y = \frac{5x}{(x+1)(x-1)}.\]
So we immediately see that \(x=-1\) and \(x=1\) are the vertical asymptotes.
In order to sketch the graph we need to determine the behaviour of the graph either side of these asymptotes.
When \(x<-1\), all three terms \(5x\), \(x+1\), \(x-1\) are all negative, so overall the function \(\dfrac{5x}{(x+1)(x-1)}\) is negative.
The sign of the function \(\dfrac{5x}{(x+1)(x-1)}\) alternates as \(x\) passes through \(-1\), \(0\) and \(1\), so it is positive in the region \(-1<x<0\), negative in the region \(0<x<1\) and positive in the region \(x>1\).
Horizontal asymptotes
As \(x\) tends to positive or negative infinity, the denominator grows much more quickly than the numerator, and so \(y\) gets closer to \(0\). Therefore \(y=0\) is a horizontal asymptote.
Intersections with axes
By looking at the equation \(y=\dfrac{5x}{x^2-1}\), we can see that \(y=0\) if and only if \(x=0\), so the only place the graph intersects the axes is at the origin \((0,0)\).
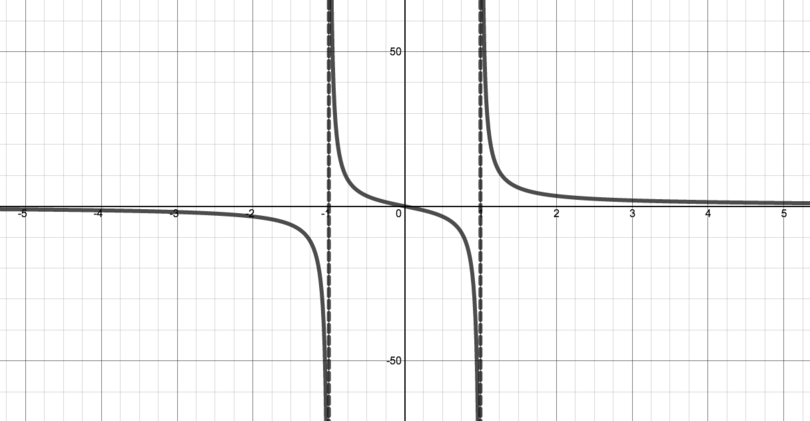
Now we have enough information to know the graph has the following shape.
Use your graph to find the number of real roots of the equation \[kx-1 = \dfrac{5x}{x^2 -1},\] when \(k\) is a positive constant.
To find the number of real roots of the equation \[kx-1 = \dfrac{5x}{x^2 -1},\] we need to find how many times \(y = kx - 1\) and \(y = \dfrac{5x}{x^2 - 1}\) intersect.
We sketch the line \(y = kx - 1\) on the previous graph for \(k > 0\), as shown.
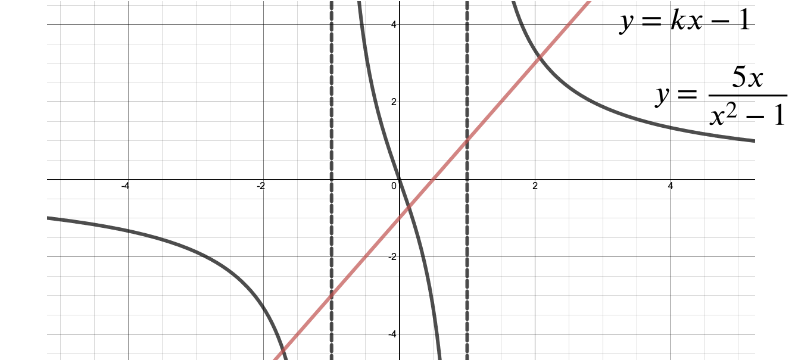
We can see from the graph that \(y = kx - 1\) and \(y = \dfrac{5x}{x^2 - 1}\) will always intersect three times if \(k\) is positive, and therefore the equation has three real roots.
Show also that there is a range of negative values of \(k\) for which the equation has only one real root. (The precise range of values of \(k\) is not required.)
Finally, we want to show that there is a range of negative values of \(k\) for which the equation has only one real root.
It’s worth noting that the equation \(kx-1 = \dfrac{5x}{x^2 -1}\) when multiplied out gives a cubic equation, and EVERY cubic equation with real coefficients has at least one real root. (Can you see why?)
For the equation to have only one real root, there must be only one point of intersection between \(y = \dfrac{5x}{x^2 - 1}\) and the line \(y = kx - 1\).
From the graph, we can see that the line \(y = kx - 1\) (for any \(k < 0\)) must always intersect \(y = \dfrac{5x}{x^2 - 1}\) exactly once in the region \(-1 < x < 1\). Therefore, for there to be only one real root, the line \(y = kx-1\) must not intersect \(y = \dfrac{5x}{x^2 - 1}\) in either of the regions \(x > 1\) or \(x < -1\). There is a range of negative values of \(k\) for which this is true, and some examples are given below.