Given that \(f(x) = x^2\) for \(-a < x \leq a\), and that \(f(x)\) is periodic with period \(2a\),
- sketch the graph of \(f(x)\) for \(-3a\leq x\leq 3a\),
Let’s start by sketching the graph of \(f(x)=x^2\) for values of \(x\) between \(-a\) and \(a\).
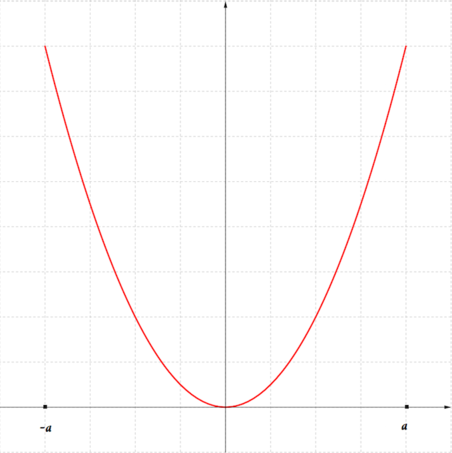
Since the function is periodic with period \(2a\), the graph of the function for \(-3a\leq x\leq 3a\) will consist of three copies of the one above, together with a single point (for \(x = -3a\)).
One copy will be for \(-3a < x\leq -a\), one for \(-a < x \leq a\), and the last one for \(a < x\leq 3a\). Therefore the graph of \(f(x)\) for \(-3a\leq x\leq 3a\) is
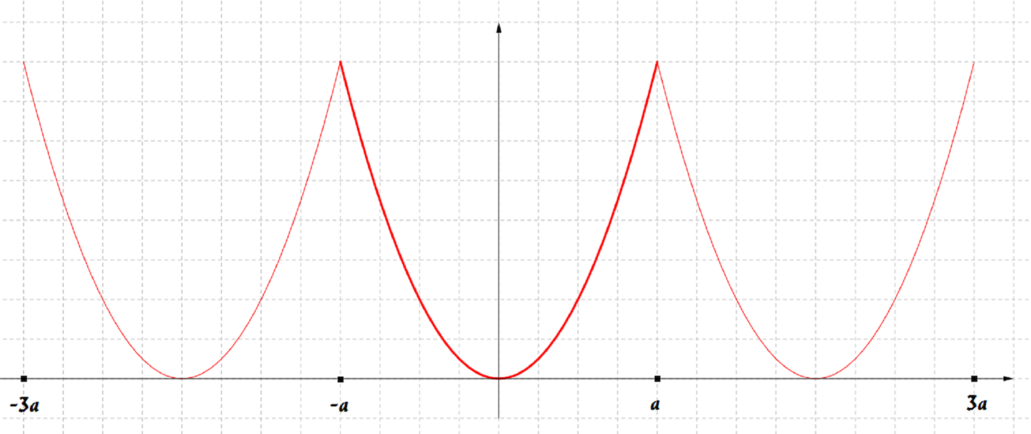
We might notice that the curve is continuous - there’s no jump from one repeat of the curve to the next, which means we can draw it without taking our pencil off the paper.
- find the general solution of the equation \(f(x)=\frac{1}{4} a^2\).
Let’s add to our graph the line \(y=\frac{1}{4}a^2\) to help us see the solution.
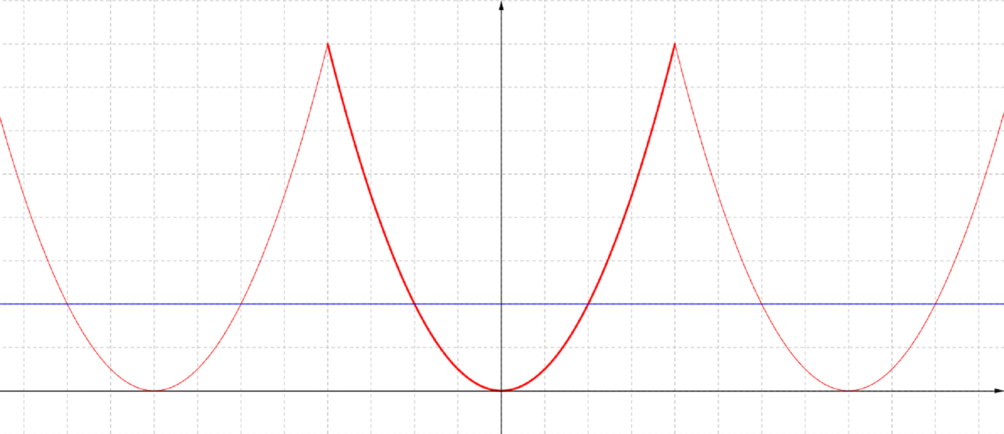
We need to solve the equation \(f(x)=\frac{1}{4} a^2\) when \(-a<x\leq a\). We have \[\frac{1}{4} a^2 = x^2 \iff x^2=\left(\frac{1}{2}a\right)^2 \iff x=\pm \frac{1}{2}a.\]
Since the function is periodic with period \(2a\), we have \(f(x)= f(x+2ak)\) for any integer \(k\) and any \(-a < x\leq a\).
So since the only solutions of \(f(x)=\dfrac{1}{4} a^2\) for \(-a<x\leq a\) are \(x=\pm \dfrac{1}{2}a\), then the solutions of \(f(x)=\dfrac{1}{4} a^2\) in general are \(\pm\dfrac{a}{2}+2ak\), where \(k\) takes integer values.

