Here is one possible way to complete the table.
| \(y\)-axis is an asymptote | Is symmetrical about \(x = 1\) | Intersects \(y\)-axis at \(3\) | Passes through origin | |
|---|---|---|---|---|
| \(x = 1\) is a root |
\(y = \dfrac{x-1}{x}\) for \(x \neq 0\) 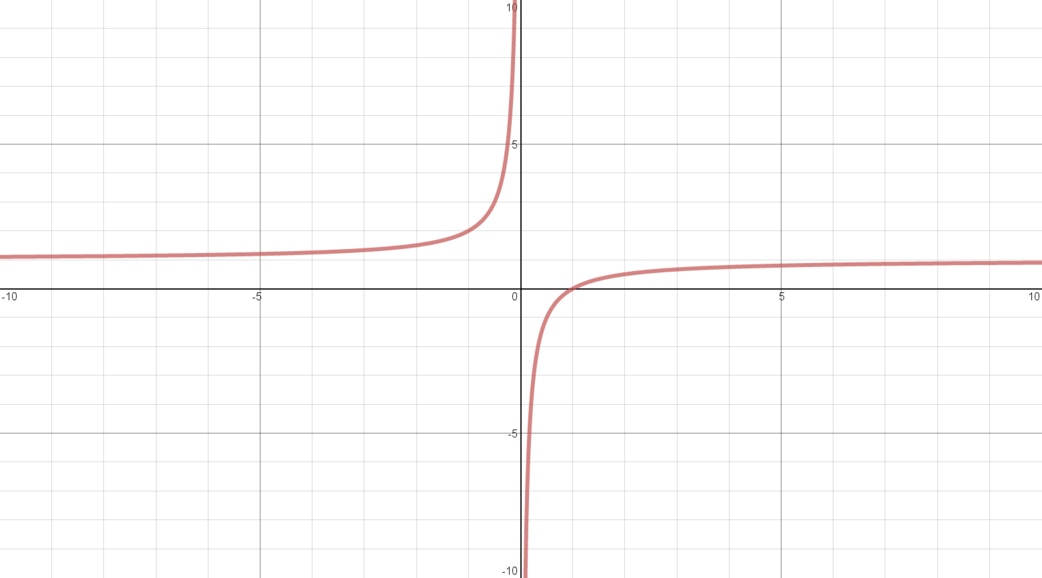
|
\(y = \vert x - 1 \vert\) 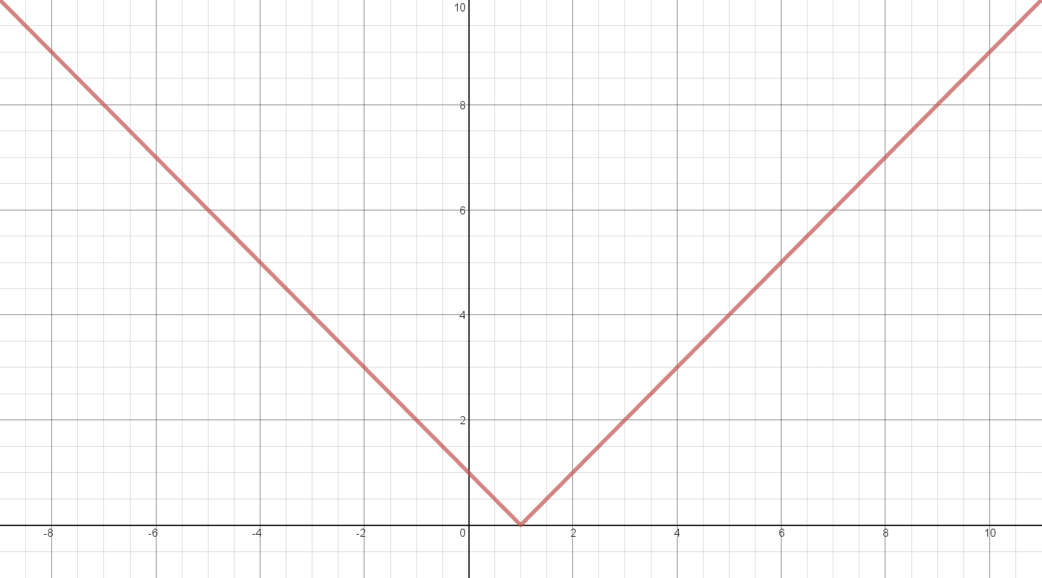
|
\(y = -3x + 3\) 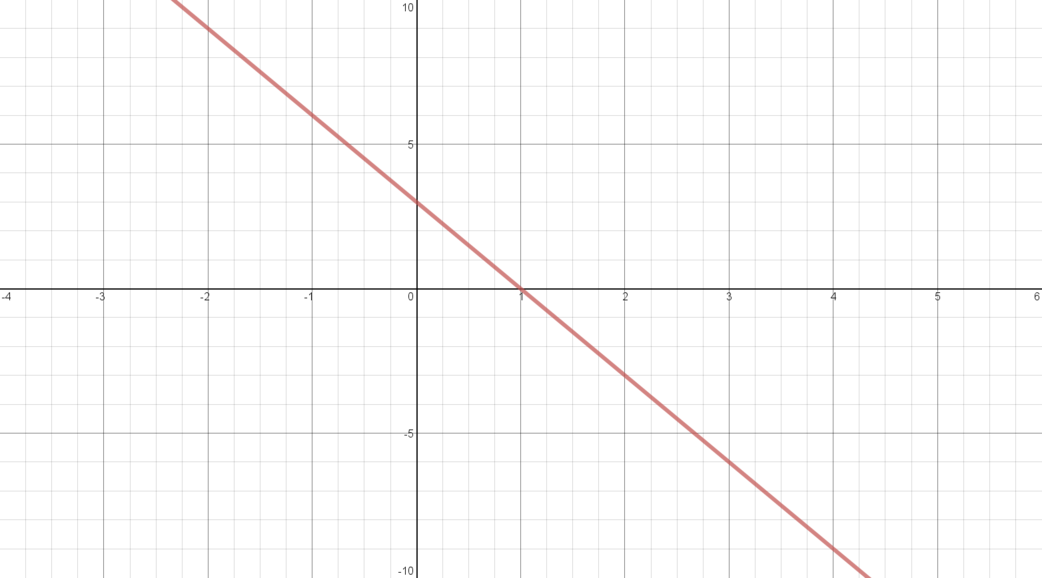
|
\(y = x(1-x)\) 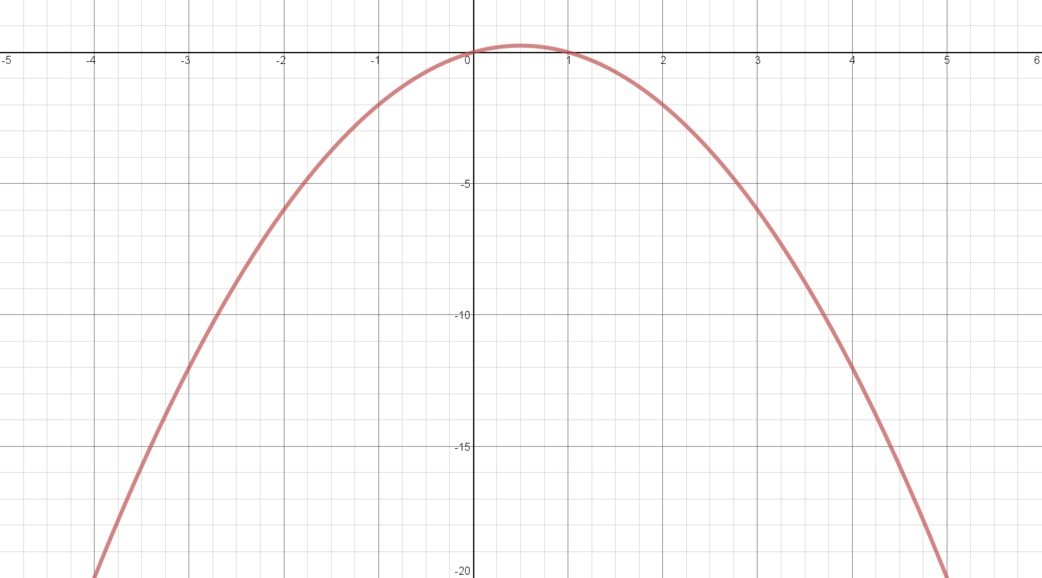
|
| Has exactly two roots. |
\(y = -1 + \dfrac{1}{x^2}\) for \(x \neq 0\) 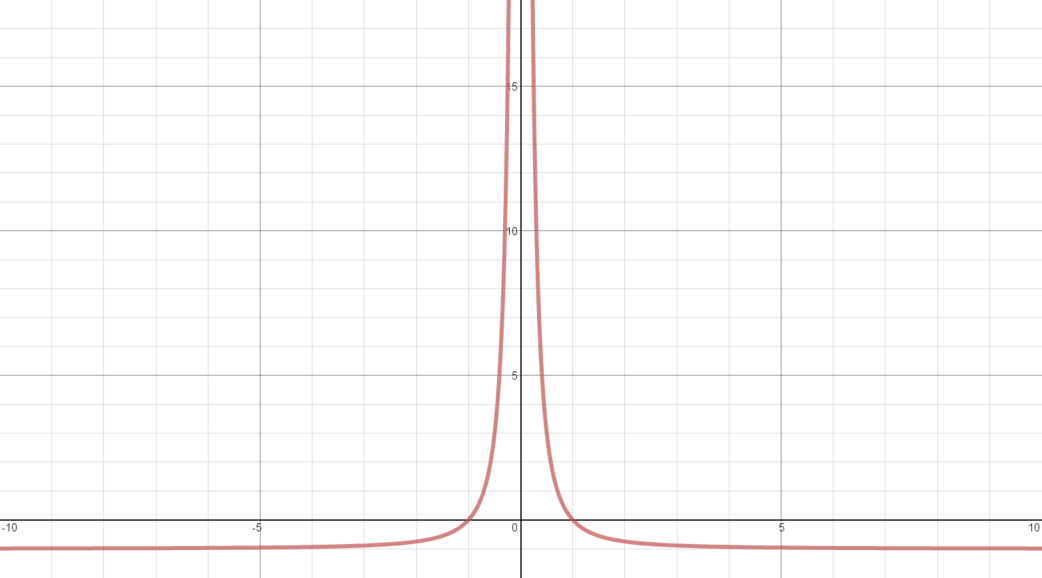
|
\(y = x(x-2)\) 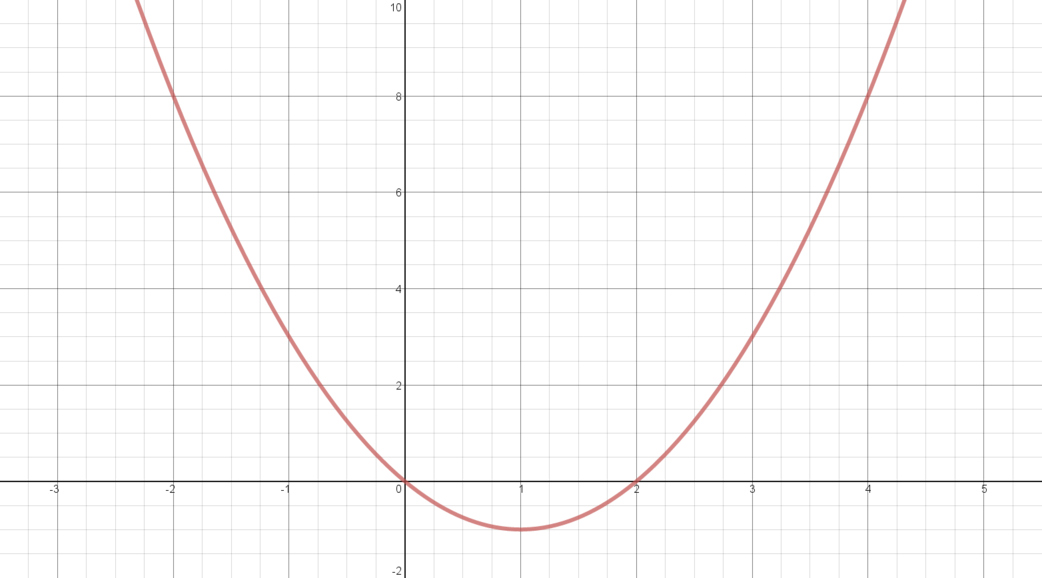
|
\(y = (x-1)^2 (x+3)\) 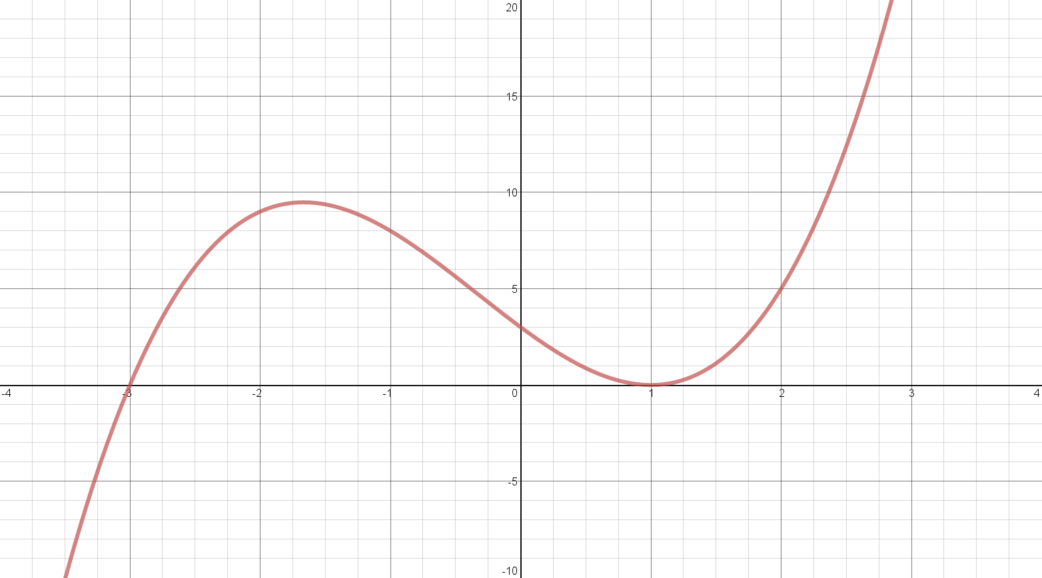
|
\(y = x(x+7)\) 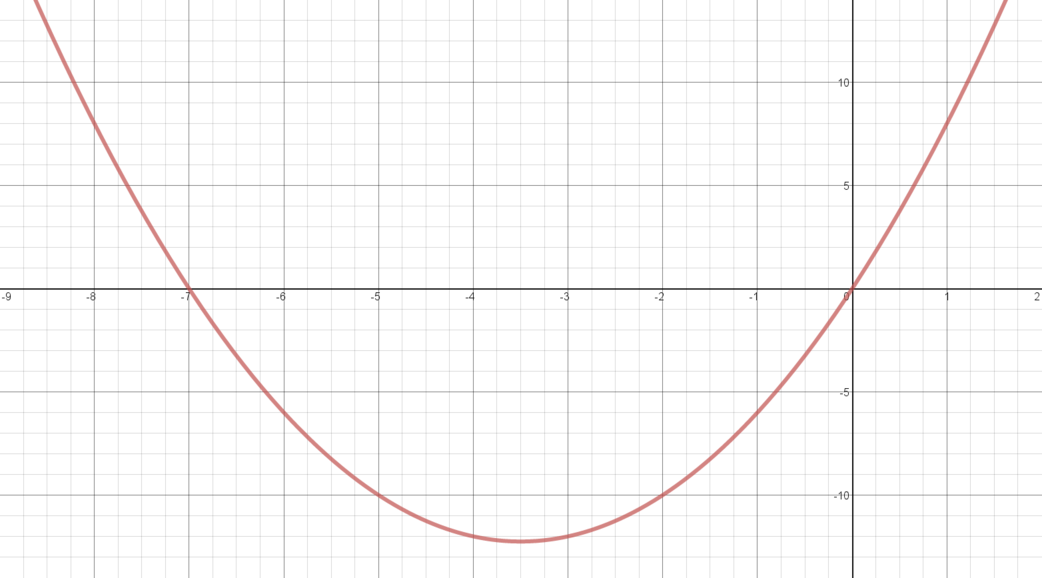
|
| \(x\)-axis is an asymptote |
\(y = \dfrac{1}{x}\) for \(x \neq 0\) 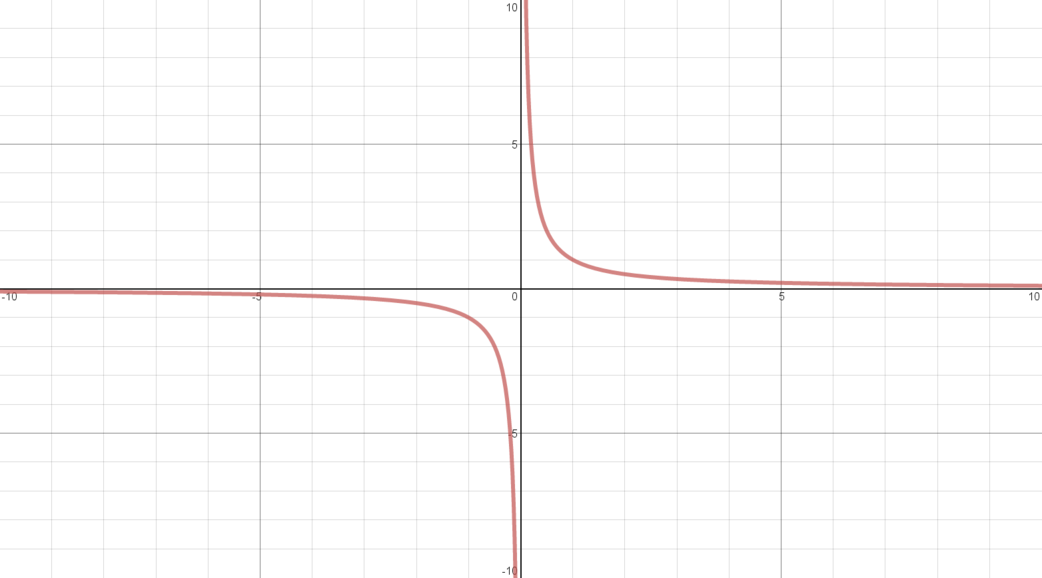
|
\(y = \dfrac{1}{(x-1)^2}\) for \(x \neq 1\) 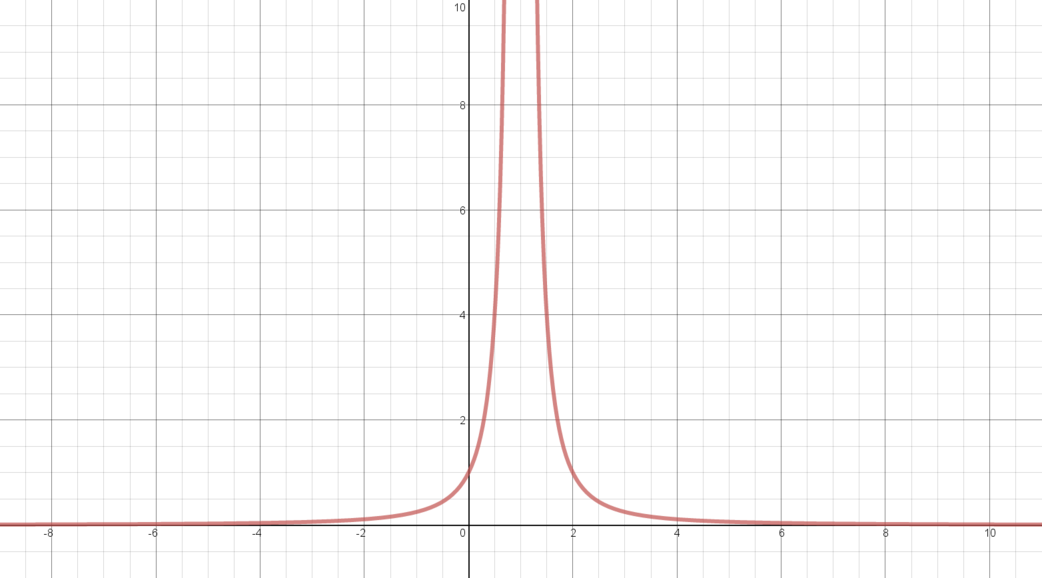
|
\(y = \dfrac{3}{x+1}\) for \(x \neq -1\) 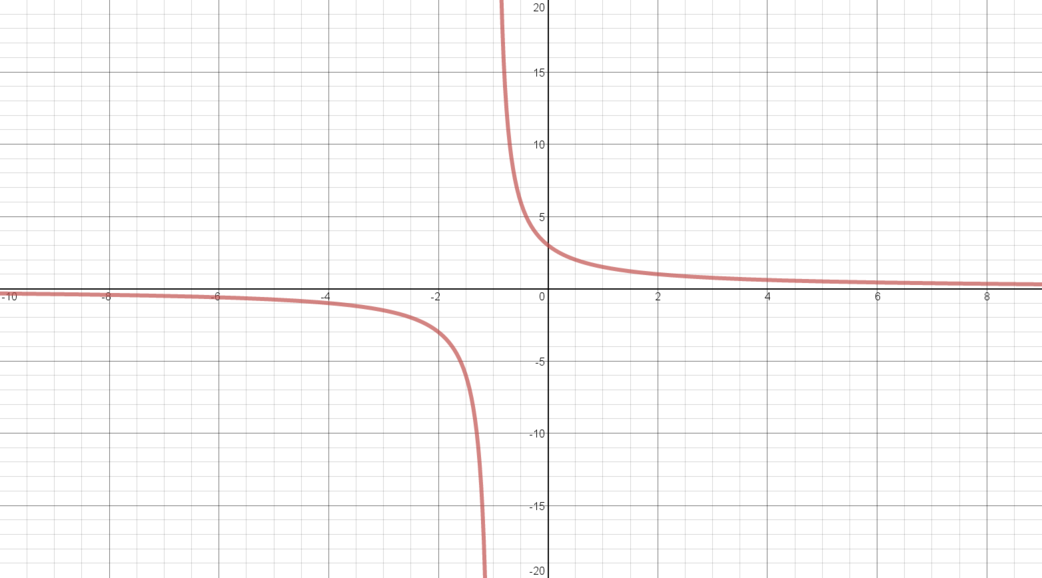
|
\(y = \dfrac{x}{(x-1)^2}\) for \(x \neq 1\) 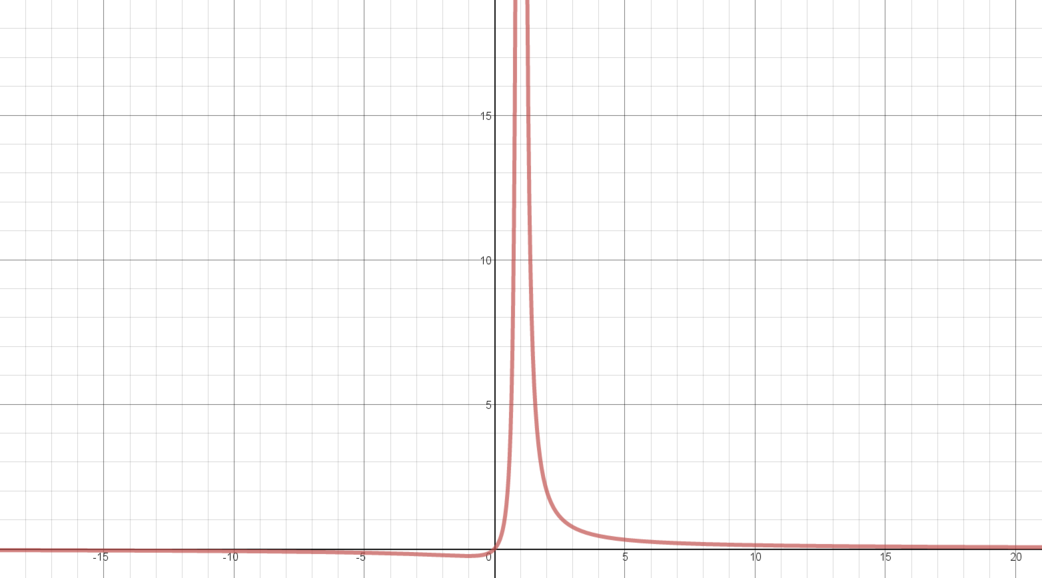
|
| \(y \to \infty\) as \(x \to \infty\) |
\(y = x + \dfrac{1}{x}\) for \(x \neq 0\) 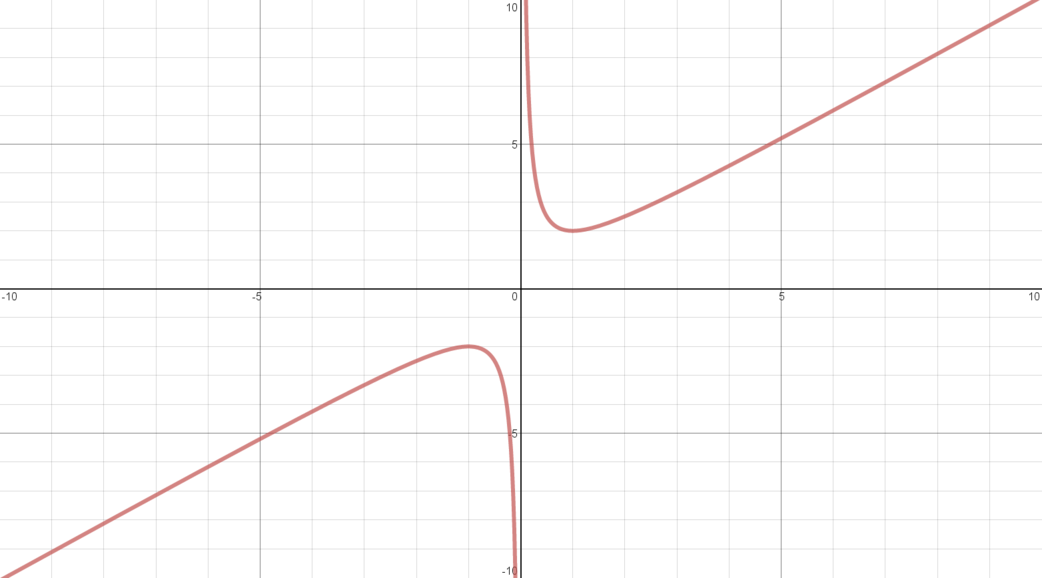
|
\(y = (x-1)^2\) 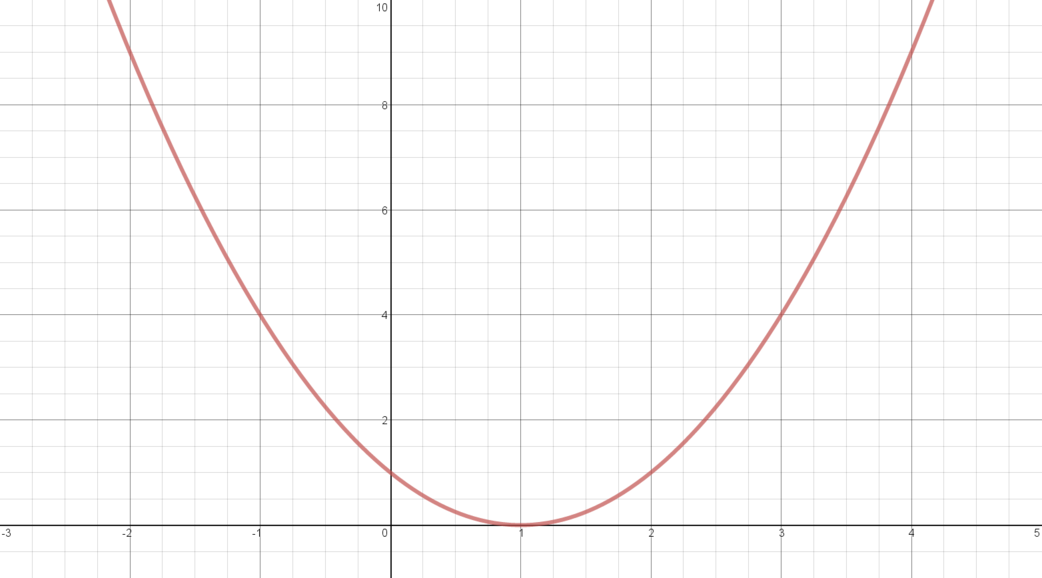
|
\(y = 2 + (x-1)^4\) 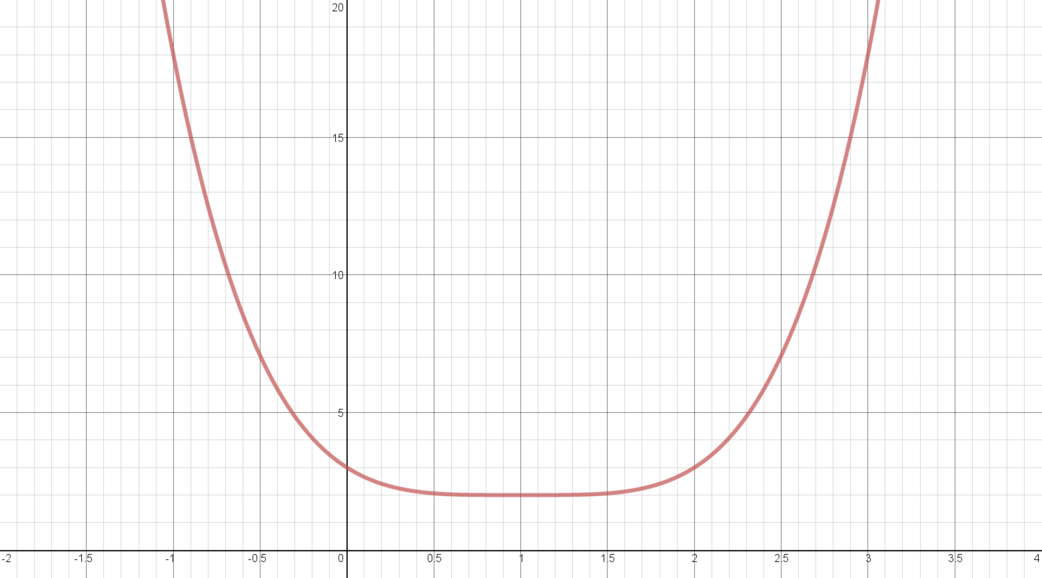
|
\(y = x\) 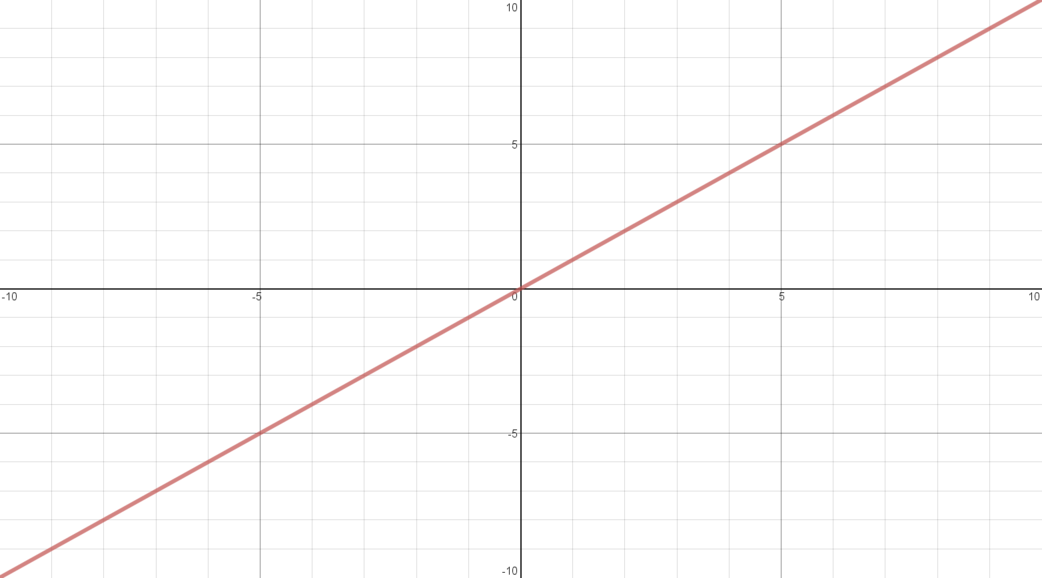
|

