Thinking about Functions
Scaffolded task

Worth 1000 words
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Problem

None of the following sketches is an accurate graph of the function \(f(x)=\dfrac{x-5}{x^2-2x-3}.\)

But which of these could be a sketch graph of \(f(x)\)?

  • Try to explain why some of the sketches can’t represent this function.
  • Which sketch graph do you think is the best representation of this function?

Once you have decided which graph(s) could represent this function, try to label key features, such as points where the graph crosses the axes. You could also try to sketch a graph that you think is a bit more true to the function than these graphs.

The sketch graphs are available separately as cards.

You may never have sketched a graph like this before, but we are asking you to think about what information the equation of the function gives you. It can be easier to think carefully about a function that you’re not familiar with.

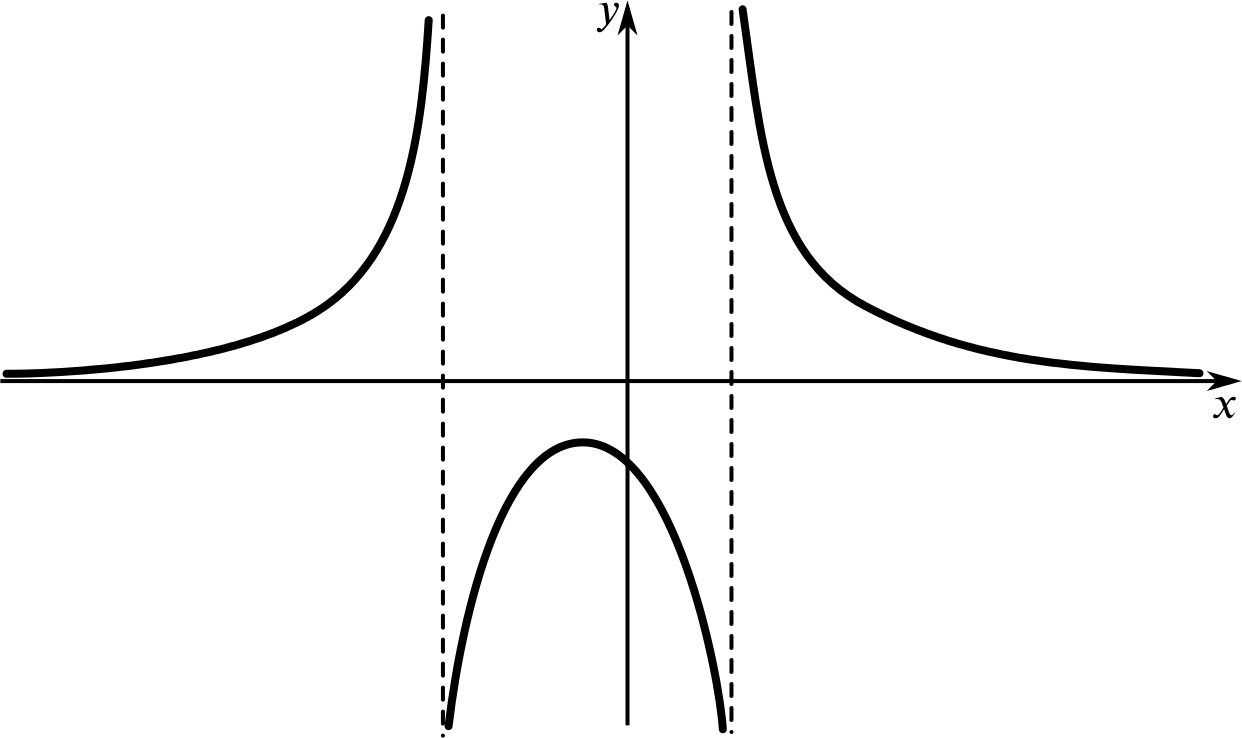
Graph with two vertical asymptotes, one just to the right of the y-axis and one to the left of the y-axis and further away. The function tends to 0 from above as x tends to both positive and negative infinity, and does not ever intersect the x-axis.
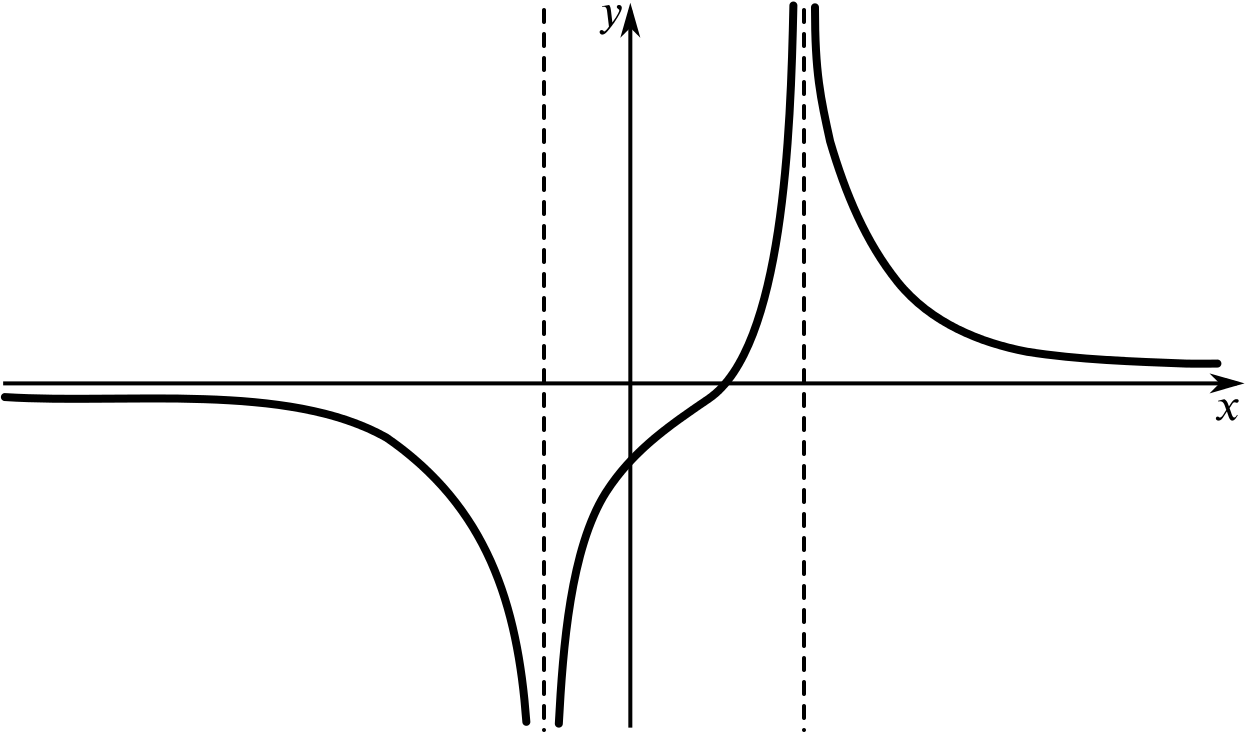
Graph with two vertical asymptotes either side of the y-axis. The curve intersects the x-axis in between these two asymptotes and tends towards the x-axis from above as x tends to positive infinity and from below as x tends to negative infinity.
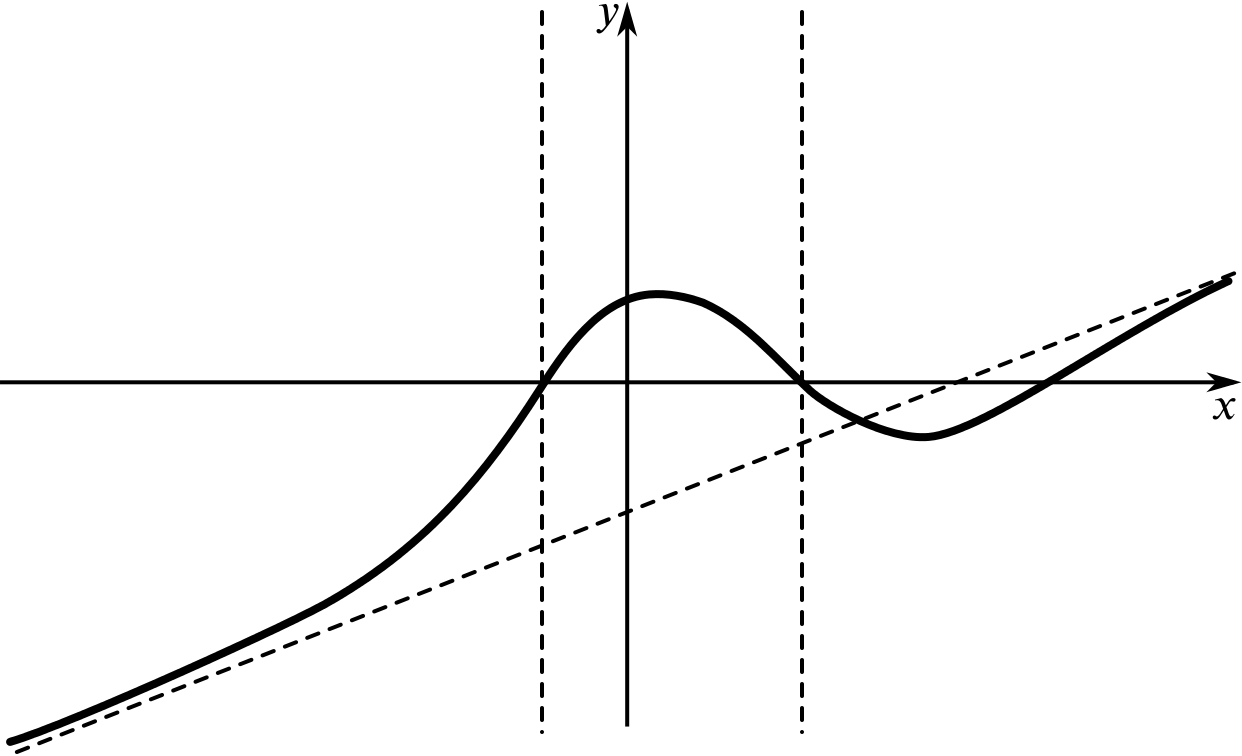
Graph with two vertical asymptotes either side of the y-axis and one positively sloped asymptote that the curve tends to as x tends to both positive and negative infinity.
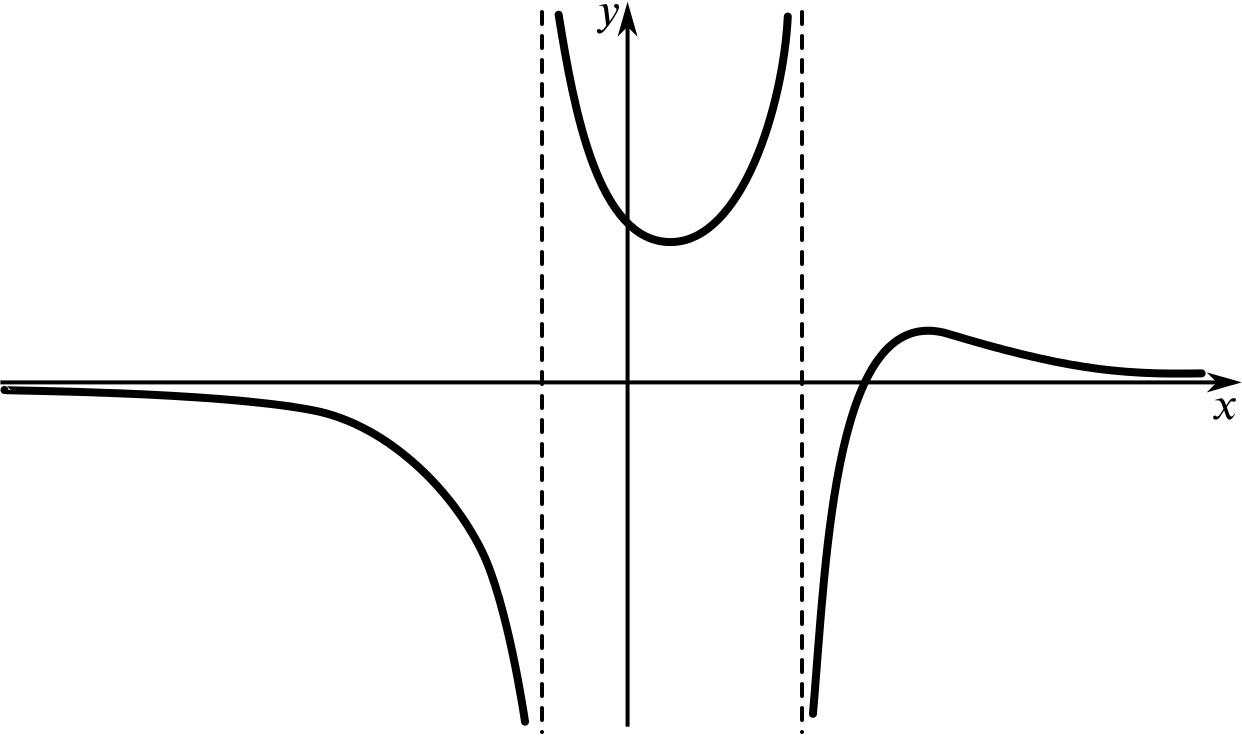
Graph with two vertical asymptotes either side of the y-axis, and intersecting the x-axis to the right of the asymptotes, and tending to 0 from below as x tends to negative infinity and from above as x tends to positive infinity.
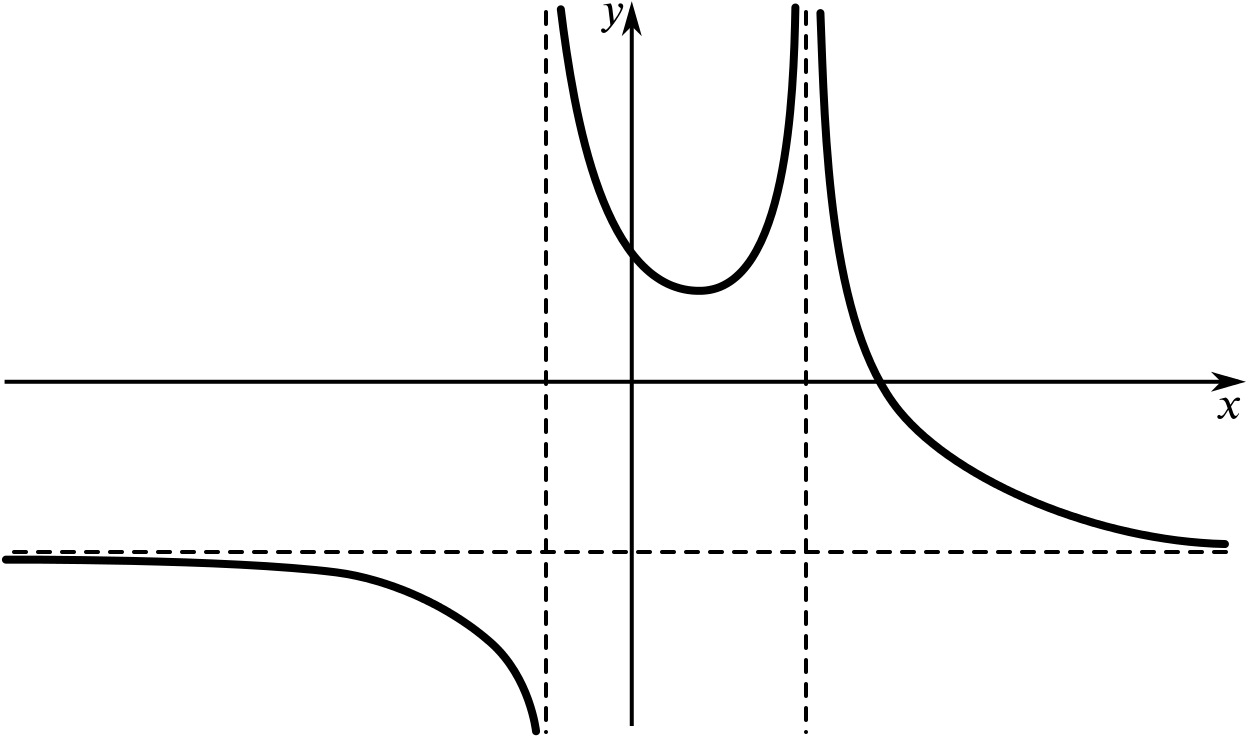
Graph with two vertical asymptotes either side of the y-axis, and one horizontal asymptote below the x-axis which the curve tends to from below as x tends to negative infinity and from above as x tends to positive infinity. The curve intersects the x-axis once to the right of the vertical asymptotes.
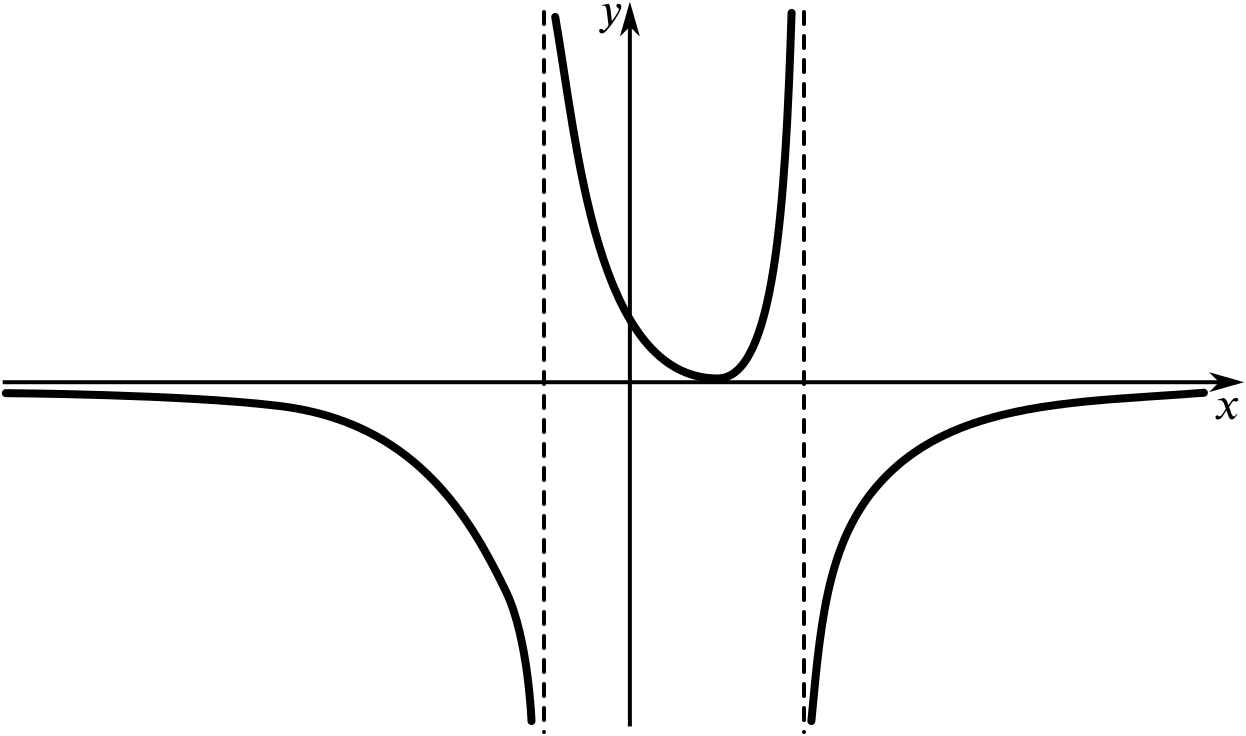
Graph with two vertical asymptotes either side of the y-axis. The curve touches the x-axis in between these asymptotes. The function tends to 0 from below as x tends to both positive and negative infinity.
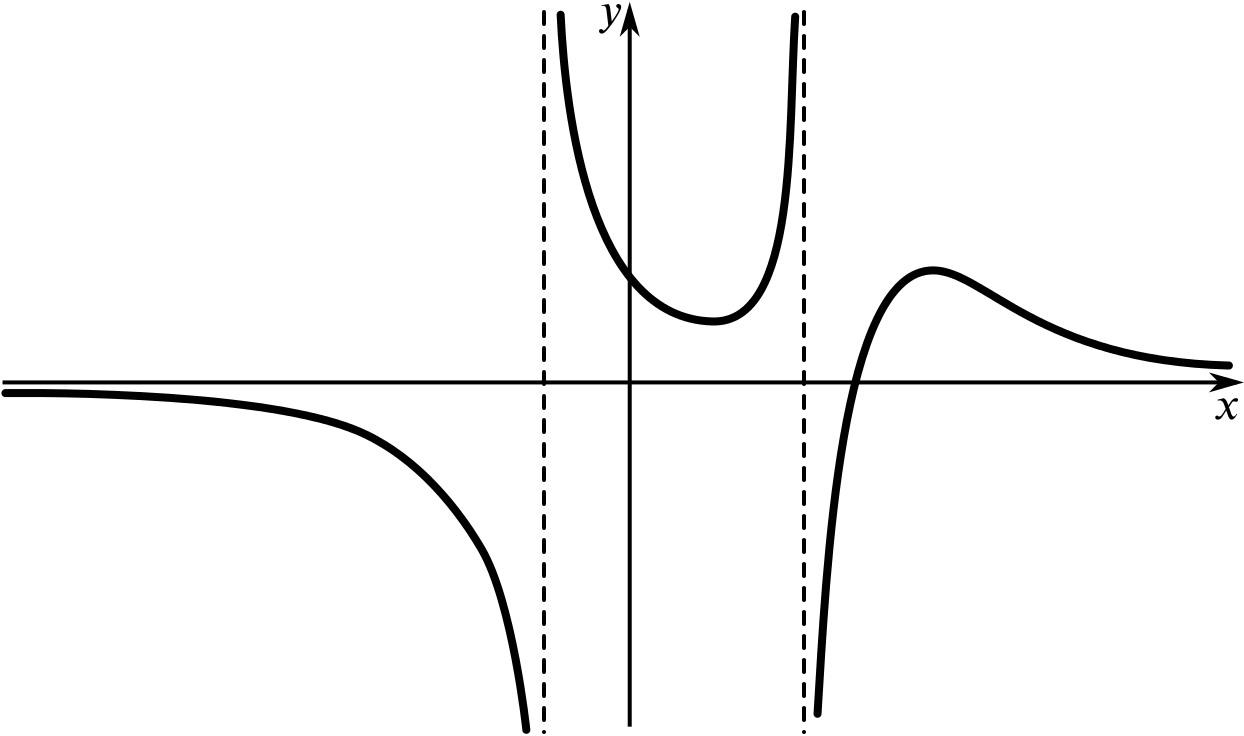
Graph with two vertical asymptotes either side of the y-axis, and intersecting the x-axis to the right of the asymptotes, and tending to 0 from below as x tends to negative infinity and from above as x tends to positive infinity. The only difference to graph D is that the maximum to the right of the asymptotes is higher
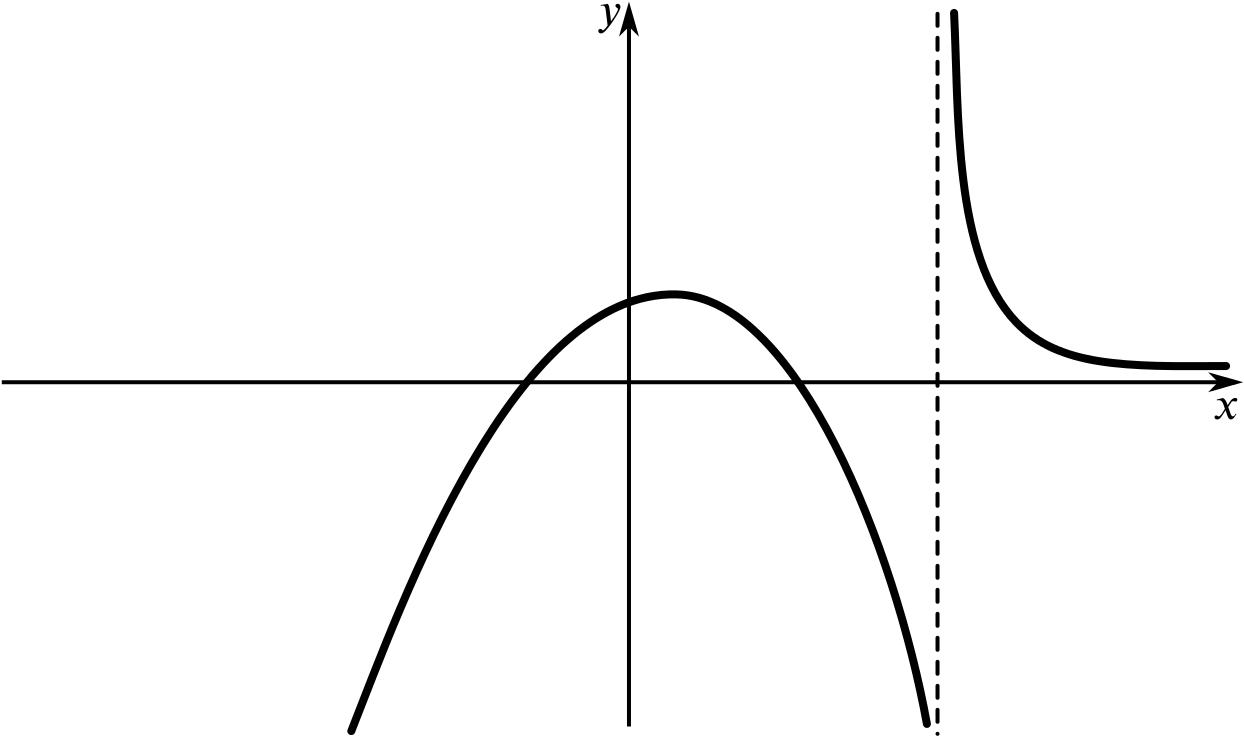
Graph with one vertical asymptote to the right of the y-axis. The curve intersects the x-axis twice, once either side of the y-axis. It tends to 0 as x tends to positive infinity and negative infinity as x tends to negative infinity.

Here are some things you might like to think about. You may think of these in a different order or you may not need to think about some of them.

  • Does the graph of \(f(x)\) cross or meet the axes? If so, where?

  • Are there any values of \(x\) for which \(f(x)\) isn’t defined? If so, what happens when \(x\) is close to these values?

  • Does the graph of \(f(x)\) have any asymptotes? If so, are these parallel to the axes? Where are they in relation to any intercepts?

  • When is the value of \(f(x)\) positive? When is it negative?

  • What happens if \(x\) has a large positive value or a large negative value?

Remember that a sketch graph needs to be as true to the function as necessary and this may depend on how we want to use the graph. It needs to show crucial features, but we don’t need to worry about exact distances and values where we don’t need them.

Previous Next
Last updated 10-Nov-16
Add to your collection Add the current resource to your resource collection
Email Twitter
Terms Cookies Privacy
Rich resources for teaching A level mathematics
Copyright © and Database Right 2013-2024 University of Cambridge
All rights reserved
University of Cambridge logo
Department for Education logo