Here is a graph showing a straight line. It is not drawn accurately. The points \((2,3)\) and \((8,8)\) lie on the line. Another point, \((4,a)\), also lies on the line. Can you work out the value of \(a\)?
How many different ways can you find to do this?
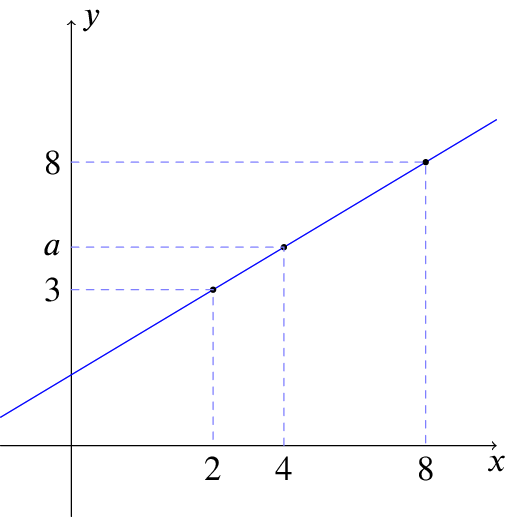
One way to do this question is to draw some similar triangles on the graph. We can then sometimes find lengths we are interested in by using properties of similar triangles.
A similar triangles method
We extend the horizontal dashed line at \(y=3\) to create some similar triangles, as shown in the following graph.
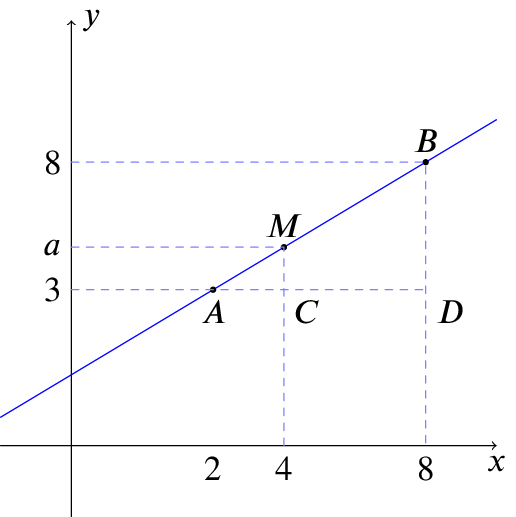
There are at least three triangles in this graph; we will focus on two of them and redraw them separately:
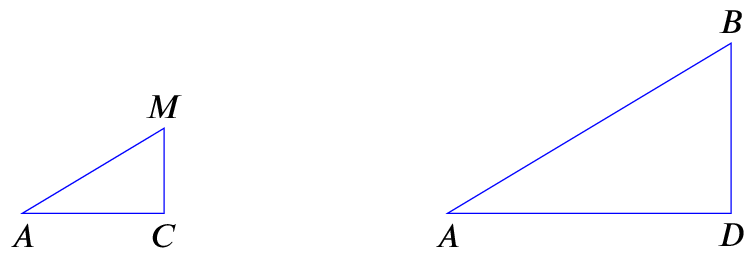
We can see that these triangles are similar, since the gradients of the sides are the same, and they are both right-angled. We can also fill in some of the side lengths we know from the triangles’ coordinates:
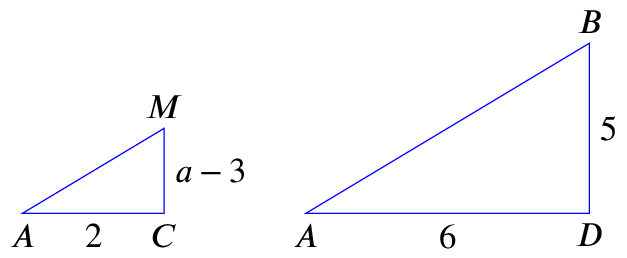
Multiplying by \(2\) gives \[a-3=\frac{5}{3}\] so \(a=\frac{14}{3}=4\frac{2}{3}\).
And this answer seems reasonable: it’s between \(3\) and \(8\), and it’s closer to \(3\).
There are several variants of this method which use slightly different choices of triangles.
A gradients method
We can think about the gradient of the line \(AB\). There are three ways to calculate it: we can find the gradient between the points \(A\) and \(B\), which is \[\frac{\text{change in $y$}}{\text{change in $x$}} = \frac{5}{6}.\] Alternatively, we can find the gradient between the points \(A\) and \(M\), which is \[\frac{a-3}{2}.\] Finally, we can find the gradient between the points \(M\) and \(B\), which gives \[\frac{8-a}{4}.\] But all of these gradients are equal, as the three points \(A\), \(B\) and \(M\) all lie on the same line. So if we take any two of them we get an equation which we can solve to find \(a\). For example, if we take the first two gradients, we get the equation \(\eqref{eq:1}\) we had before, so again we find that \(a=\frac{14}{3}\).
The equation of the line method
Another way of doing this question is to work out the equation of the line \(AB\) (see Geometry of Equations for more on finding equations of straight lines).
The gradient of the line is \[\frac{8-3}{8-2}=\frac{5}{6}.\] So the equation of the line is \(y=\frac{5}{6}x+c\). To find \(c\), we know that it passes through the point \((2,3)\), so we can substitute in to get \(3=\frac{5}{6}\times 2+c\), so \(c=\frac{4}{3}\).
(Alternatively, we can use the general form of a straight line with gradient \(m\) passing through a given point, namely \(y-y_1=m(x-x_1)\). This gives us \(y-3=\frac{5}{6}(x-2)\), which we can rearrange if we wish to again get \(y=\frac{5}{6}x+\frac{4}{3}\).)
We can now substitute in \(x=4\) to work out the value of \(y\), which gives \(y=\frac{5}{6}\times 4+\frac{4}{3}=\frac{14}{3}\), so \(a=\frac{14}{3}\).
We have described three different approaches to finding the value of \(a\). Do you prefer one of these approaches to the other? If so, why?
- This time, the \(x\)-coordinate of one of the points is missing—can you work it out?
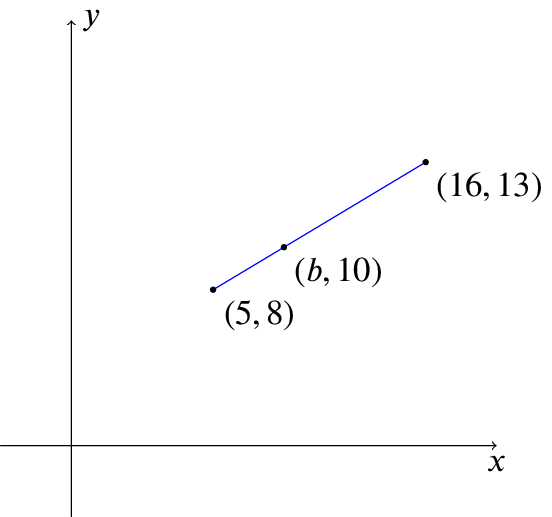
Did all of your approaches from question 1 work, or did some not? Or perhaps they worked with some modification?
Can you find any new ways to do this question which are different from your methods for question 1?
The idea here is the same. We will use the similar triangles approach, and draw in the same triangles on the graph as we did in question 1:
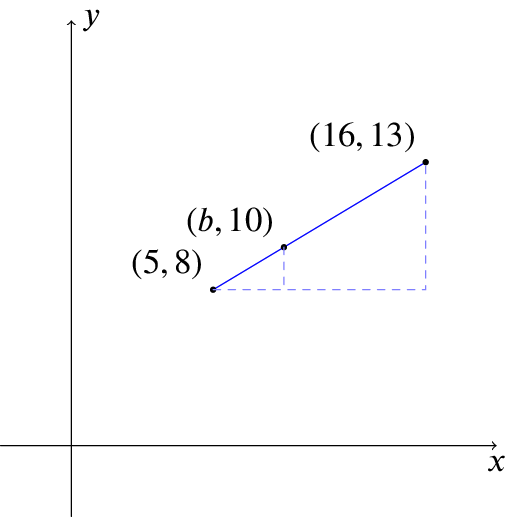
Again, we can draw out the two triangles separately to get a clearer picture of what’s going on. This time, we won’t label all of the points with letters, as it’s clear now where they come from.
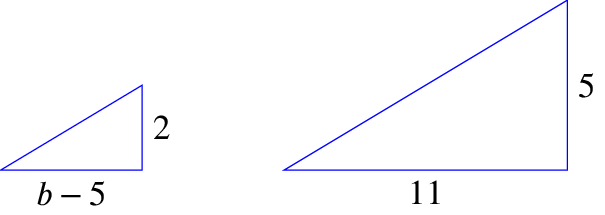
Then comparing the ratios of the sides gives the equation \[\frac{b-5}{2} = \frac{11}{5}\] so that \(b-5=\frac{22}{5}\), which brings us to \(b=\frac{47}{5}=9\frac{2}{5}=9.4\).
Note that for this question, we wrote the ratios with the \(x\)-coordinates on the tops of the fractions, as this is where the unknown \(b\) is—this just makes our life easier when we go to work out \(b\).
- This time, you might find it helpful to draw your own sketches. Give your answers to 1 decimal place.
You had to draw your own sketch and the numbers are nastier! But it’s exactly the same idea still. We’ll show the sketch graphs here, but not the individual triangles.
- The point \((7.3, c)\) lies on the straight line joining \((4.1, 37)\) and \((8.9, 63)\). Find \(c\).
The sketch is:
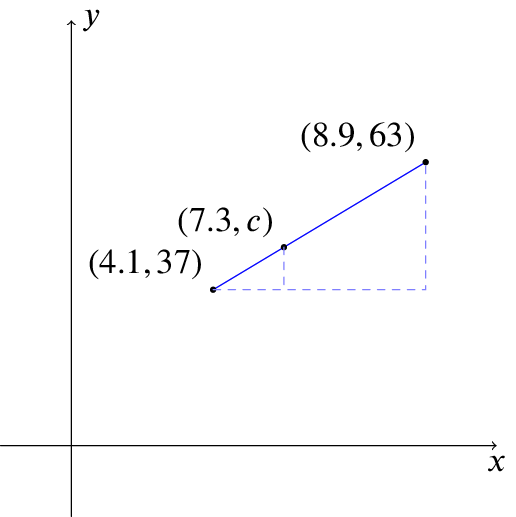
Then comparing the similar triangles gives the equation \[\frac{c-37}{7.3-4.1} = \frac{63-37}{8.9-4.1}\] and working out the calculations gives \[\frac{c-37}{3.2} = \frac{26}{4.8} = 5.416\ldots,\] so \(c=3.2\times5.416\ldots+37=54.3\) to 1 d.p.
Note that we did not round \(\frac{26}{4.8}\) to \(5.417\) in the middle of the calculation; it is better to keep numbers unrounded on your calculator and only round the final answer, as this prevents errors from accumulating.
- The point \((d, 47.5)\) lies on the straight line joining \((15.05, 42)\) and \((17.55, 56)\). Find \(d\).
This time, the sketch is:
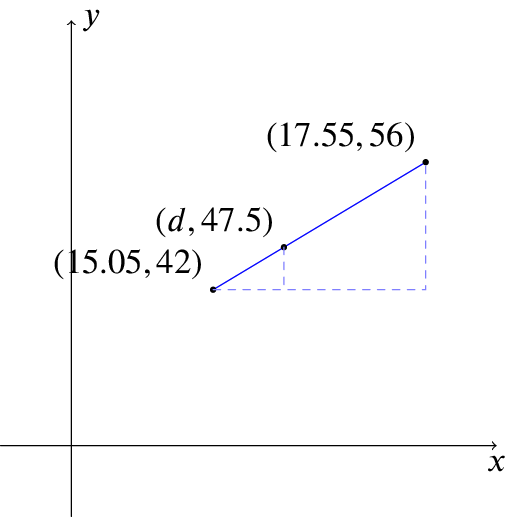
so the corresponding equation is \[\frac{d-15.05}{47.5-42} = \frac{17.55-15.05}{56-42}.\] Working things out as before gives \[\frac{d-15.05}{5.5} = \frac{2.5}{14}=0.178\ldots\] so \(d=5.5\times 0.178\ldots+15.05=16.0\) to 1 d.p.
- The point \((12, e)\) lies on the straight line joining \((8, 20)\) and \((17, 1)\). Find \(e\).
This time, the sketch is
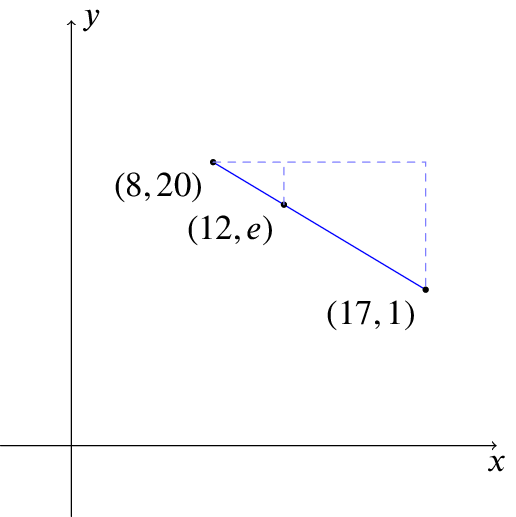
Now the gradient is negative, but the method works in exactly the same way, as long as we take care. We should also double-check that our final answer makes sense!
If we compare the lengths of the triangle sides, we have \[\frac{20-e}{12-8} = \frac{20-1}{17-8},\] so \[\frac{20-e}{4} = \frac{19}{9},\] yielding \(20-e=8.444\dots\), so \(e=11.6\) to 1 d.p., and this seems sensible, as \(11.6\) is between \(20\) and \(1\), and close to half way between them.
This does seem a little bit confusing, though, since we have to think carefully about which way round to subtract each pair of coordinates to ensure we get a positive number – it does lead to a significant potential for mistakes. Thinking about gradients instead might make our life somewhat easier here.
Here is an alternative using gradients: equating the gradient between the points \((8,20)\) and \((12,e)\) with the gradient between \((8,20)\) and \((17,1)\) gives \[\frac{e-20}{12-8} = \frac{1-20}{17-8},\] so \[\frac{e-20}{4} = \frac{-19}{9},\] yielding \(e-20=-8.444\dots\), so \(e=11.6\) to 1 d.p.
This way, the signs took care of themselves, and we could have done the problem without drawing a sketch, had we been so inclined.

