An island is in the shape of a convex polygon with perimeter \(p\) miles. Its territorial water consists of all points of the sea within \(r\) miles of its coast. Assuming that no other land is within \(r\) miles of the island and that the earth is flat, prove that the area of the territorial water is \((pr+\pi r^2)\) square miles.

Let’s draw a diagram of a convex polygon, and see if we can draw a boundary around it.
We can begin to draw the points that are \(r\) away from the polygon.
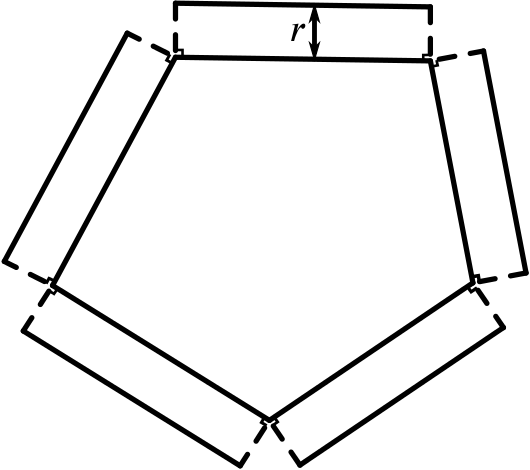
It is harder at the vertices of the polygon, but if we draw part of a circle of radius \(r\) at each vertex, we find all points \(r\) away from the polygon.
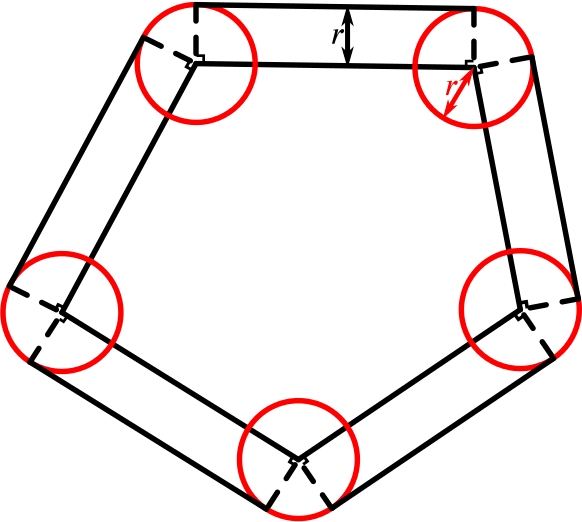
From our diagram, we can see that the total area of the rectangles is \(pr\) (if we cut them out and laid them next to each other, the length would be the perimeter of the polygon), so we just need to find the area of the circle sectors.
To do this, we must find the interior angles. We know that the sum of the interior angles of a polygon with \(n\) sides is \(180(n-2)\).
Therefore, if we cut out all of the circle sectors and put them together, the total angle of the sector we find in degrees would be \[360n -180n-180(n-2)\] (that is, the total degrees in the circle at each vertex, minus the two right angles from the rectangles, minus the interior angles of the polygon).
But this is equal to \(360^\circ\), so the sectors make a circle of radus \(r\), which has area \(\pi r^2\). So the formula for the area of the terratorial waters is \[ pr+\pi r^2. \]Consider whether the same formula would hold (a) if the island were convex but not polygonal,
Let’s test an example. The circle is an example of a convex shape that isn’t polygonal.

A circle of perimeter \(p\) has radius \(\dfrac{p}{2\pi}\), therefore the territorial waters have area \[ \pi\left(\frac{p}{2\pi}+r\right)^2-\pi\frac{p^2}{4\pi^2}=pr+ \pi r^2, \] therefore the formula holds for a circle.
Let’s take any convex shape. We can approximate the shape by a convex polygon by taking some points on its edge and joining them with straight lines.

The more vertices in the convex polygon, the closer the polygon to the convex shape.

The formula we found in the first part of the question holds for any such approximation. In fact, since the formula does not depend on \(n\) (the number of vertices), we can let \(n\) tend to infinity and the formula will not change.
As \(n\) tends to infinity the polygon tends to the non-polygonal convex shape, and since the formula we found in the first part holds for each \(n\), it will hold in the limit too.
Therefore the formula still holds in this case.
We require the vertices to be ‘reasonably spread out’ for this to happen.
Consider whether the same formula would hold (b) if it were polygonal but not convex.
Let’s try a simple example to see if there is any hope of the formula holding.
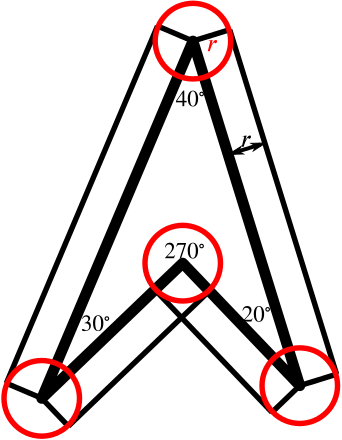
We can see from this picture that the rectangles here have area \(pr-r^2\), and the circle sectors have area \(\pi r^2\dfrac{140+150+160}{360}\), and so the area of the territiorial waters in this case is \[ pr-r^2+\pi r^2+\frac{\pi r^2}{4}. \] Therefore the formula does not hold in this case.

