An irregular hexagon with all sides of equal length is placed inside a square of side length \(1\), as shown below (not to scale). What is the length of one of the hexagon sides?
(a) \(\sqrt{2} - 1,\quad\) (b) \(2 - \sqrt{2},\quad\) (c) \(1,\quad\) (d) \(\dfrac{\sqrt{2}}{2},\quad\) (e) \(2 + \sqrt{2}\).
Let’s call the length of the hexagon sides \(x\). We can now add some lengths to the diagram.
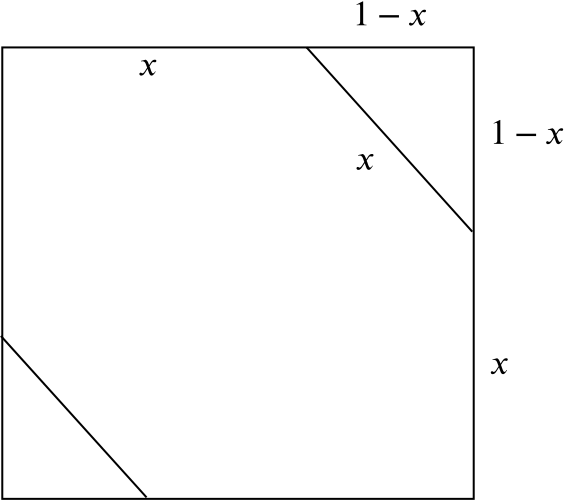
The triangles in the corners are isosceles and right-angled so their sides are in the ratio \(1:1:\sqrt{2}\). So we have \[\frac{x}{1-x} = \sqrt{2} \quad\implies\quad x=\frac{\sqrt{2}}{1+\sqrt{2}} = 2-\sqrt{2}\] and the answer is (b).

