The sum of the lengths of the \(12\) edges of a cuboid is \(\quantity{x}{cm}\). The distance from one corner of the cuboid to the furthest corner is \(\quantity{y}{cm}\). What in \(\mathrm{cm^2}\) is the total surface area of the cuboid?
(A) \(\quad \dfrac{x^2-2y^2}{2} \qquad\) (B) \(\quad x^2+y^2 \qquad\) (C) \(\quad \dfrac{x^2-4y^2}{4} \qquad\) (D) \(\quad \dfrac{xy}{6} \qquad\) (E) \(\quad \dfrac{x^2-16y^2}{16}\)
Let the sides of the cuboid be \(a\), \(b\) and \(c\).
This means the total edge-length, \(x = 4(a+b+c)\).
The length of the longest possible diagonal is, by Pythagoras, \(y = \sqrt{a^2 + b^2 + c^2}\).
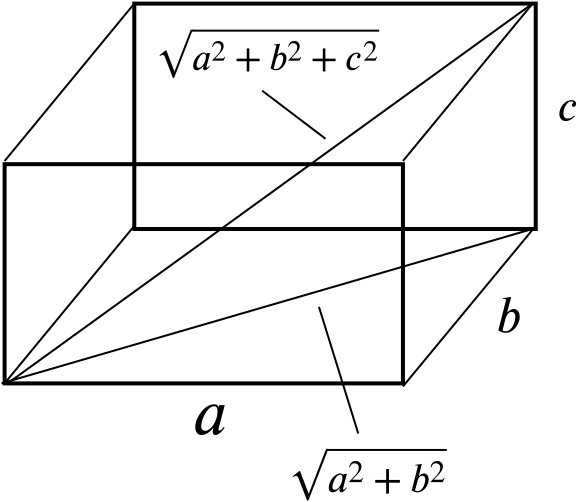
The surface area we seek is \(A=2(ab+bc+ca)\).
We need to find a relationship between \(x\), \(y\) and \(A\). Thinking about the units or dimensions of each quantity, we have \([x]=[y]=[L]\) and \([A]=[L^2]\) which suggests we should be interested in \(x^2\) and \(y^2\). We have \[x^2=16(a+b+c)^2 = 16(a^2+b^2+c^2+2ab+2bc+2ca) = 16(y^2+A).\] Hence we have \[A=\frac{x^2-16y^2}{16}\] and the answer is (E).

