The point lying between \(P(2,3)\) and \(Q(8,-3)\) which divides the line \(PQ\) in the ratio \(1:2\) has co-ordinates
\((4,-1)\)
\((6,-2)\)
\((\frac{14}{3}, 2)\)
\((4,1)\)
Approach 1: Similar triangles
We sketch the situation:
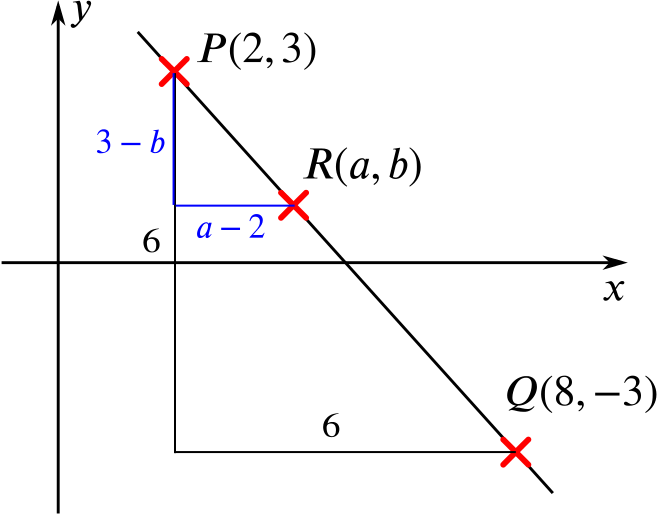
Let \(R = (a,b)\) divide the line \(PQ\) in the ratio \(1:2\) with \(PR:RQ = 1:2\), so \(R\) lies one third of the way along \(PQ\).
By similar triangles, \(\dfrac{PR}{PQ} = \dfrac{1}{3} = \dfrac{a-2}{6}=\dfrac{3-b}{6}\), which gives \(a = 4\), \(b =1\).
Approach 2: Vectors
We can also answer this question using vectors.
Now \(\vec{OP} = \begin{pmatrix}2\\3\end{pmatrix}\), while \(\vec{OQ} = \begin{pmatrix}8\\-3\end{pmatrix}\).
Hence \(\vec{PQ} = \vec{OQ} - \vec{OP} = \begin{pmatrix}6\\-6\end{pmatrix}\).
Now \(\vec{OR}= \vec{OP} + \frac{1}{3}\vec{PQ} = \begin{pmatrix}2\\3\end{pmatrix}\) + \(\begin{pmatrix}2\\-2\end{pmatrix}=\begin{pmatrix}4\\1\end{pmatrix}\).
Either way, we reach the answer d.

