A sphere of radius \(\quantity{6}{cm}\) fits inside a cone of vertical angle \(84^\circ\), so that \(BA\) is a tangent to the sphere.
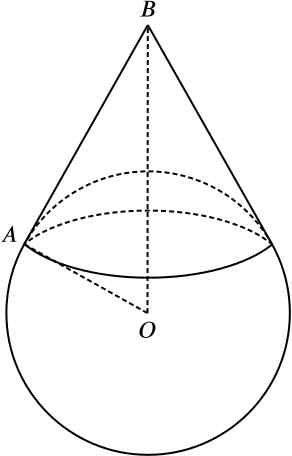
Calculate
- the length \(AB\);
Since \(AB\) is tangent to the sphere, \(\angle BAO = 90^\circ\). We are also given that \(OA=6\), and that the vertical angle of the cone is \(84^\circ\), so \(\angle OBA = 42^\circ\), giving us
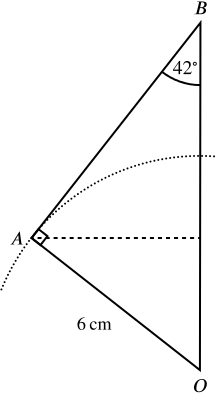
Now \[ \tan 42^\circ = \frac{\text{$OA$}}{\text{$AB$}} \implies \text{$AB$} = \frac{6}{\tan 42^\circ} = \quantity{6.66}{cm}. \]
- the radius of the base of the cone;
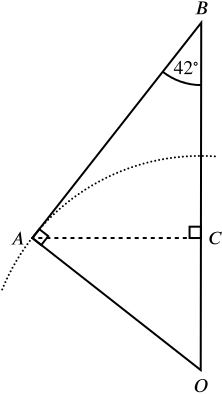
- the shortest distance from \(B\) to the sphere;
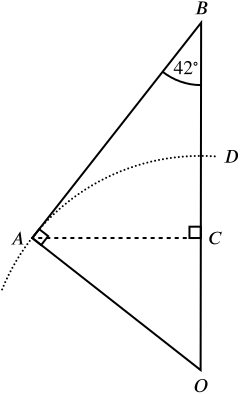
The point \(D\) is the one on the sphere closest to B, so our goal is to find \(BD\). We have \(OD=6\), since it’s a radius of the sphere, and hence \[ \text{$BD$} = \text{$BO$} - 6. \] So we need to calculate the length of \(BO\). Considering \(\triangle AOB\), we have that \[ \sin 42^\circ = \frac{\text{$AO$}}{\text{$BO$}} \implies \text{$BO$} = \frac{6}{\sin 42^\circ} \] and therefore \[ \text{$BD$} = \frac{6}{\sin 42^\circ} - 6= \quantity{2.97}{cm}. \]
- the volume of the cone.

