Take a look at the image below.
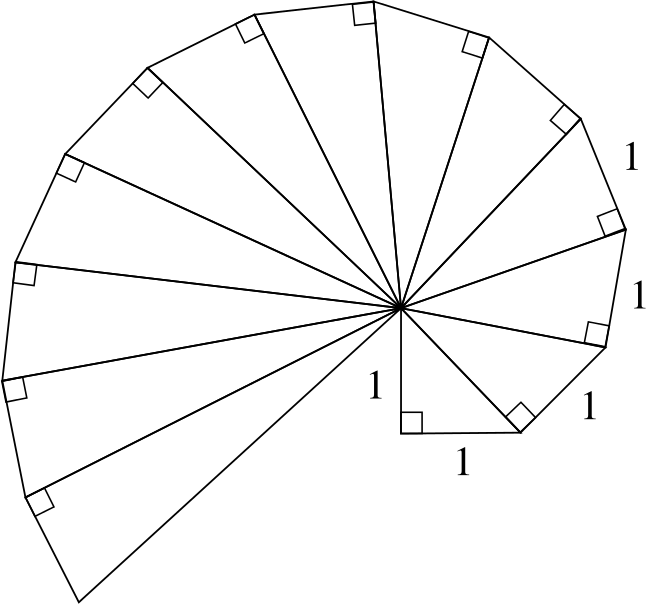
What do you make of it?
What questions might you ask yourself about this image?
Here are some questions we asked about this image that you might like to think about, if you have not already considered them.
Can I recreate the image using only straight-edge and compasses?
Can I find line segments of lengths \(2\), \(3\), \(4\), \(\dots\)?
Are there any lengths that do not occur in the diagram?
How many steps would I need to construct \(\sqrt{5}\) in the diagram?
Can I construct \(\sqrt{13}\) in any other way (using straight-edge and compasses)?
Which other lengths can I construct in other ways (using straight-edge and compasses)?
How will the spiral change if I start with a \(2\times 2\) right-angled triangle instead?
How will the spiral change if I start with a right-angled triangle that isn’t isosceles?

