Take a look at the image below.
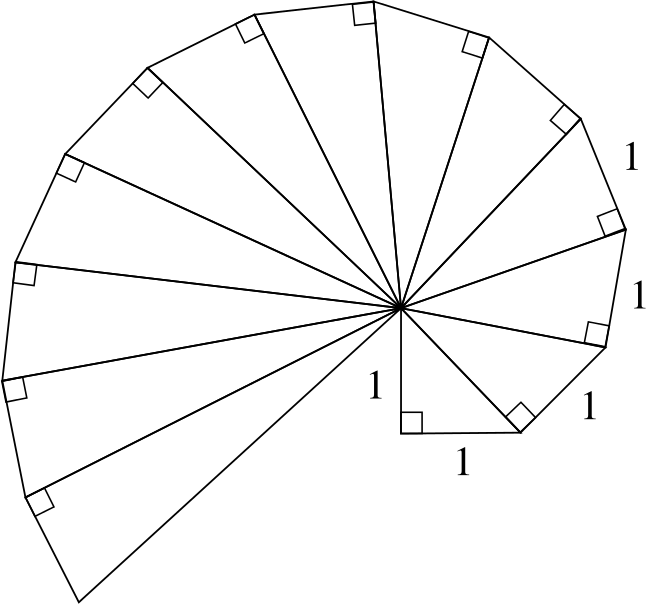
What do you make of it?
Can I find line segments of lengths \(2\), \(3\), \(4\), \(\dots\)?
How many steps would I need to construct \(\sqrt{5}\) in the diagram?
Are there any lengths that do not occur in the diagram?
One side of each right-angled triangle is always of length \(1\) and the side perpendicular to this is equal to the hypotenuse of the previous triangle.
Starting with the \(1\times 1\) triangle I can use Pythagoras’ theorem to calculate the length of the hypotenuse to be \(\sqrt{2}\). Therefore the perpendicular side lengths of the second triangle in the spiral are \(1\) and \(\sqrt{2}\).
Repeating this process shows me that the length of the second hypotenuse is \(\sqrt{3}\), the third is \(\sqrt{4}\), the fourth is \(\sqrt{5}\), and so on.
I notice that the third hypotenuse is of length \(\sqrt{4}=2\). Given that the sequence of hypotenuse lengths will continue I predict that the \(8\)th hypotenuse will have a length of \(\sqrt{9}=3\) and the \(15\)th will have a length of \(\sqrt{16}=4\). The whole number lengths appear further and further apart as the spiral continues.
Can I construct a length of \(\sqrt{13}\) in any other way (using straight-edge and compasses)?
Which other lengths can I construct in other ways (using straight-edge and compasses)?
Each of the lengths in this image is created using the previous triangle. So to get to \(\sqrt{13}\) I had to construct \(12\) triangles in the spiral.
If I want to construct a length of \(\sqrt{13}\) directly then I could do this if \(\sqrt{13}\) is the hypotenuse of a right-angled triangle with integer side lengths. I would then require that \(a^2+b^2=13\) where \(a\) and \(b\) are integers. This can be satisfied if I take \(a=2\) and \(b=3\).
The question of whether I can construct other lengths in different, potentially more efficient ways, is less obvious. I saw that it was possible to produce a length of \(\sqrt{13}\) by constructing a single right-angled triangle. Perhaps it makes sense to start by considering other lengths that can be constructed using a single right-angled triangle. Then to produce a length \(n\) we require that \(a^2+b^2=n^2\) where \(a\) and \(b\) are integers, so for example \(\sqrt{8}\) can be produced by taking \(a=b=2\).
It is interesting to notice here that I am saying that \(\sqrt{8}\) can be produced from an enlargement (scale factor \(2\)) of the original \(1\times 1\) right-angled triangle. From this I can deduce that \(\sqrt{8}=2\sqrt{2}\).
Perhaps this is useful to help me identify some other lengths that can be produced by enlarging the original \(1\times 1\) right-angled triangle.
I need to be aware that I cannot produce all lengths by constructing a single right-angled triangle. For example, there are no integer values for \(a\) and \(b\) that will satisfy \(a^2+b^2=6\). However, this does not mean that I cannot construct lengths like this more efficiently than in the spiral.
If we take \(\sqrt{12}\) then in the spiral I would need to construct \(11\) right-angled triangles to reach it. However, if I construct a \(2\times 2\) right-angled triangle and then a second right-angled triangle from this of side lengths \(2\) and \(\sqrt{8}\) then I produce \(\sqrt{12}\).
Alternatively I could construct a right-angled triangle with a base length of \(2\) and a hypotenuse of \(4\). The remaining side length would be \(\sqrt{12}\) as required.
If I want to construct a right-angled triangle with a base length of \(2\) and a hypotenuse of \(4\), using straight-edge and compasses, then it might help to think of it as half of an equilateral triangle of side length \(4\). Once I’ve constructed this equilateral triangle I can bisect an angle and extend the line to the opposite side to create the required right-angled triangle.
How will the spiral change if I start with a \(2\times 2\) right-angled triangle instead?
I began to answer this question above, when I realised that \(\sqrt{8}\) could be constructed from a \(2\times 2\) right-angled triangle. Assuming that the spiral will have the property that every triangle will have one constant side length of \(2\) then I get hypotenuse lengths of \(\sqrt{8}\), \(\sqrt{12}\), \(\sqrt{16}\), \(\sqrt{20}\), \(\sqrt{24}\), and so on. This time the values inside the square roots are going up in fours (compared to ones in the original image). This is to be expected as the constant side length is \(2\) and the next hypotenuse is given by \(a^2+2^2=c^2\).
It is also interesting to notice that this sequence could be written as \(2\sqrt{2}\), \(2\sqrt{3}\), \(2\sqrt{4}\), \(2\sqrt{5}\), \(2\sqrt{6}\), \(\dots\)
How will the spiral change if I start with a right-angled triangle that isn’t isosceles?
If I start with a \(1\times 2\) right-angled triangle then my first hypotenuse length is \(\sqrt{5}\). If my spiral continues to follow the pattern of keeping one side length constant then this spiral will progress in a similar way to the \(2\times 2\) spiral considered above: \(\sqrt{5}\), \(\sqrt{9}\), \(\sqrt{13}\), \(\sqrt{17}\), \(\dots\)
I wonder what would happen if the spiral did not have a constant side length…

