Suppose that \(a\), \(b\), \(c\) are integers such that \[a \sqrt{2} + b = c \sqrt{3}.\]
- By squaring both sides of the equation, show that \(a = b = c = 0\).
[You may assume that \(\sqrt{2}, \sqrt{3}\) and \(\sqrt{2/3}\) are all irrational numbers. An irrational number is one which cannot be written in the form \(p/q\) where \(p\) and \(q\) are integers.]
Squaring both sides of the equation gives \[2a^2 + 2ab\sqrt{2} + b^2 = 3c^2.\]
If \(ab \neq 0\) then \[\sqrt{2} = \frac{3c^2 - 2a^2 - b^2}{2ab},\] but this is a contradiction because \(\sqrt{2}\) is irrational and so cannot be written in the form \(\dfrac{p}{q}\) for integers \(p\) and \(q\).
So we must have either \(a=0\) or \(b=0\).
If \(a=0\), then the initial equation becomes \(b=c\sqrt{3}\). Either we have \(b=c=0\) or \(\sqrt{3}=b/c\). The latter is impossible because \(\sqrt{3}\) is irrational.
Similarly, if \(b=0\), then the initial equation becomes \(a \sqrt{2}=c \sqrt{3}\). Again, we either have \(a=c=0\) or \(\sqrt{2/3}=c/a\). The latter is impossible as \(\sqrt{2/3}\) is irrational.
So either way, we must have \(a = b = c = 0\).
- Suppose now that \(m\), \(n\), \(M\), \(N\) are integers such that the distance from the point \((m,n)\) to \((\sqrt{2},\sqrt{3})\) equals the distance from \((M,N)\) to \((\sqrt{2},\sqrt{3})\).
Show that \(m=M\) and \(n=N\).
Given that the distance from the point \((m,n)\) to \((\sqrt{2},\sqrt{3})\) equals the distance from \((M,N)\) to \((\sqrt{2},\sqrt{3})\), we have \[(m-\sqrt{2})^2 + (n-\sqrt{3})^2 = (M-\sqrt{2})^2 + (N-\sqrt{3})^2,\] which after rearranging becomes \[2\sqrt{2}(M-m) + (m^2 + n^2 - M^2 - N^2) = 2\sqrt{3}(n-N).\]
Now this is in the same form as the given initial equation, with \[\begin{align*} a &= 2(M-m), \\ b &= (m^2 + n^2 - M^2 - N^2), \\ c &= 2(n-N). \end{align*}\]From the first part of the question, we know that \(a=b=c=0\), and so we have \[2(M-m) = 0 = 2(n-N),\] and hence \(m=M\) and \(n=N\).
Given real numbers \(a\), \(b\) and a positive number \(r\), let \(N(a,b,r)\) be the number of integer pairs \(x\), \(y\) such that the distance between the points \((x,y)\) and \((a,b)\) is less than or equal to \(r\). For example, we see that \(N(1.2,0,1.5)=7\) in the diagram below.

- Explain why \(N(0.5,0.5,r)\) is a multiple of \(4\) for any value of \(r\).
If a particular point \((x,y)\) is within a distance \(r\) of \((\frac{1}{2},\frac{1}{2})\), then so are its reflections in the lines \(x=\frac{1}{2}\), \(y=\frac{1}{2}\), and in both lines.
These are the points \((1-x,y)\), \((x,1-y)\) and \((1-x,1-y)\) respectively.
No points with integer coordinates can lie on these reflection lines.
So the points with integer coordinates that are a maximum distance of \(r\) away from \((\frac{1}{2},\frac{1}{2})\) can be split into \(4\) sets of equal size by the lines \(x=\frac{1}{2}\) and \(y=\frac{1}{2}\), as shown in the diagram below.
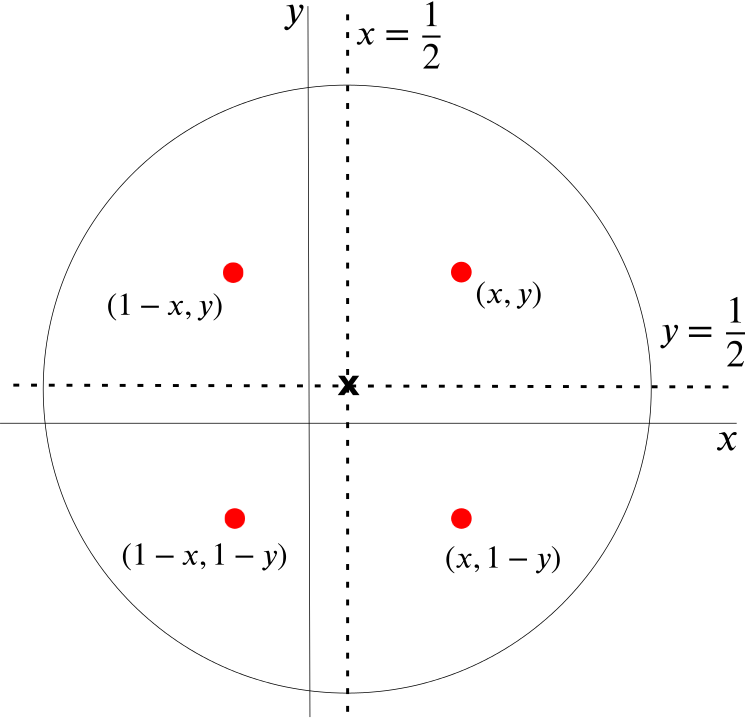
Hence \(N(0.5,0.5,r)\) must be a multiple of \(4\).
- Let \(k\) be any positive integer. Explain why there is a positive number \(r\) such that \(N(\sqrt{2},\sqrt{3},r)=k\).
As \(r\) increases, the circle grows and contains more lattice points (points with integer coordinates), without limit.
But in part (ii), we showed that there are no two lattice points equidistant from \((\sqrt{2},\sqrt{3})\), so the circle must only ‘consume’ one lattice point at a time.
Hence \(N(\sqrt{2},\sqrt{3},r)\) can take any positive integer value.

