- Show that \(\theta=18^\circ\) satisfies the equation \(\cos 3\theta=\sin 2\theta\).
We know that \[\cos(3\times 18^\circ)=\cos 54^\circ=\sin(90^\circ-54^\circ)=\sin 36^\circ=\sin(2 \times 18^\circ).\] So \(\theta=18^\circ\) satisfies \[\cos 3\theta=\sin2\theta.\]
By expressing \(\cos 3\theta\) and \(\sin 2\theta\) in terms of trigonometrical functions of \(\theta\), show that \(\sin 18^\circ\) is a root of the equation \[4x^2+2x-1=0,\] …
We can express both \(\cos3\theta\) and \(\sin2\theta\) in terms of just \(s = \sin\theta\) and \(c = \cos\theta\).
We’ll use the identities \[\sin2\theta=2sc,\] \[\cos2\theta=1-2s^2\] and \[\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta.\]
We have \[\cos3\theta=\cos(2\theta+\theta)=\cos(2\theta) c-\sin(2\theta) s = (1-2s^2)c - 2scs = c(1-4s^2).\]
So if \(\sin2\theta-\cos3\theta=0\), we have \(2sc-c(1-4s^2)=0\), or \(c(4s^2+2s-1)=0.\)
Now we know that \(\sin(18^\circ)\) is a solution to this equation, and so \(\sin(18^\circ)\) is a root of \(4x^2+2x-1=0\), since \(\cos18^\circ\ne0\).
Hence find its value as a surd.
We complete the square in order to find the roots of \(4x^2+2x-1\) in surd form. We have \[4x^2+2x-1=\left(2x+\frac{1}{2}\right)^2-\frac{5}{4}=0,\] so that \[2x+\frac{1}{2}=\pm\frac{\sqrt{5}}{2},\] and we have \[x=\frac{-1\pm\sqrt{5}}{4}.\] Finally, we must choose whether we need a plus or a minus sign to find the root corresponding to \(\sin18^\circ\). We know that \(\sin18^\circ>0\), so we choose the plus sign. So we have that \[\sin18^\circ=\frac{-1+\sqrt{5}}{4}.\]
Find all solutions between \(0^\circ\) and \(360^\circ\) of the equation \[4\tan 2x=\cot x.\]
We play a similar game here to that of the first part of the question. Firstly, we can write \[\tan x=\frac{s}{c}, \quad \cot x=\frac{1}{\tan x}=\frac{c}{s},\] so the equation we need to solve becomes \[4\frac{\sin(2x)}{\cos(2x)}=\frac{c}{s} \implies 4\sin(2x)s-\cos(2x)c=0 \implies 8s^2c-(1-2s^2)c=0 \implies (10s^2-1)c=0.\] So we have that \(\cos x=0\) solves this, which gives us the values \(x=90^\circ, 270^\circ\) between \(0^\circ\) and \(360^\circ\). We also have that \[\sin x=\pm\frac{1}{\sqrt{10}}\] is a solution, so that \(x=\sin^{-1}(\pm1/\sqrt{10})\) are also solutions. To work out how many solutions between \(0^\circ\) and \(360^\circ\), consider
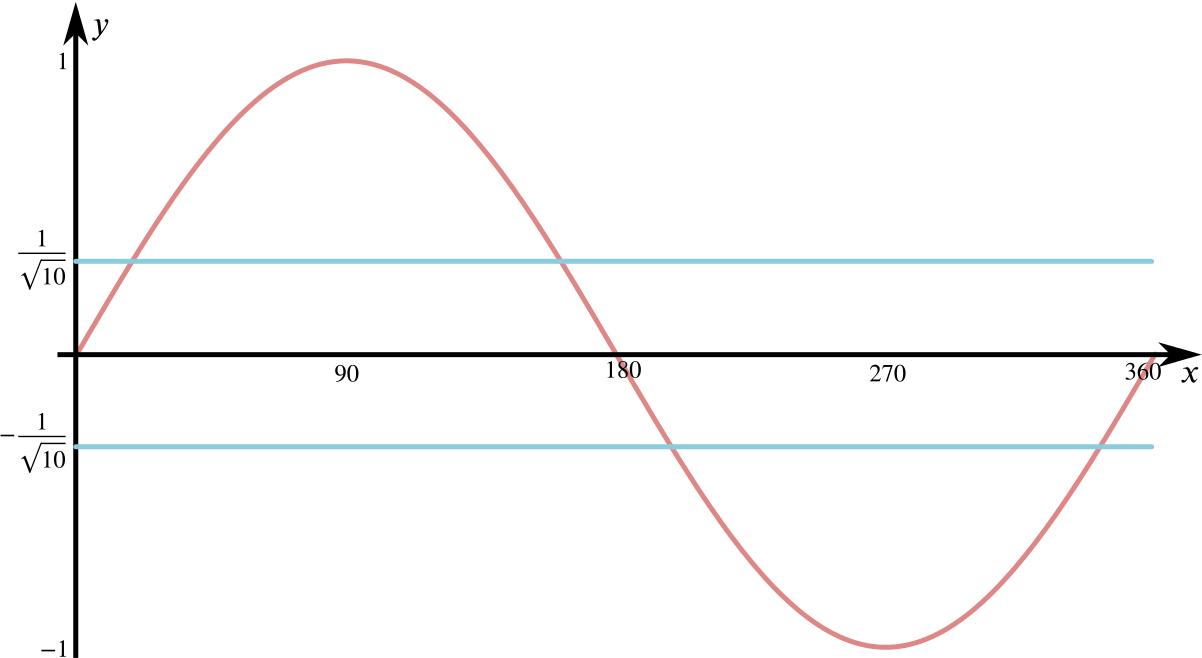
We see that \(\sin x=\pm1/\sqrt{10}\) four times between \(0^\circ\) and \(360^\circ\).
Using a calculator, one finds that \(\sin^{-1}(1/\sqrt{10})=18.4^\circ\) to one decimal place. From the symmetries of sine, we see that the other angles are then \(180^\circ-18.4^\circ=161.6^\circ\), \(180^\circ+18.4^\circ=198.4^\circ\) and \(360^\circ-18.4^\circ=341.6^\circ\), giving us six solutions in total.

