Exit fullscreen mode

Trigonometry: Compound Angles

Transformation... or not?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Further questions

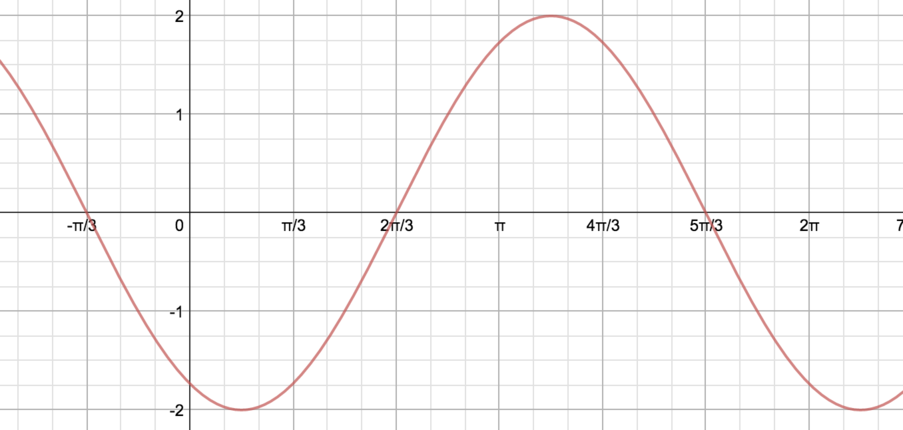
Below is the graph of \(y=3\sin x+4\cos x\).

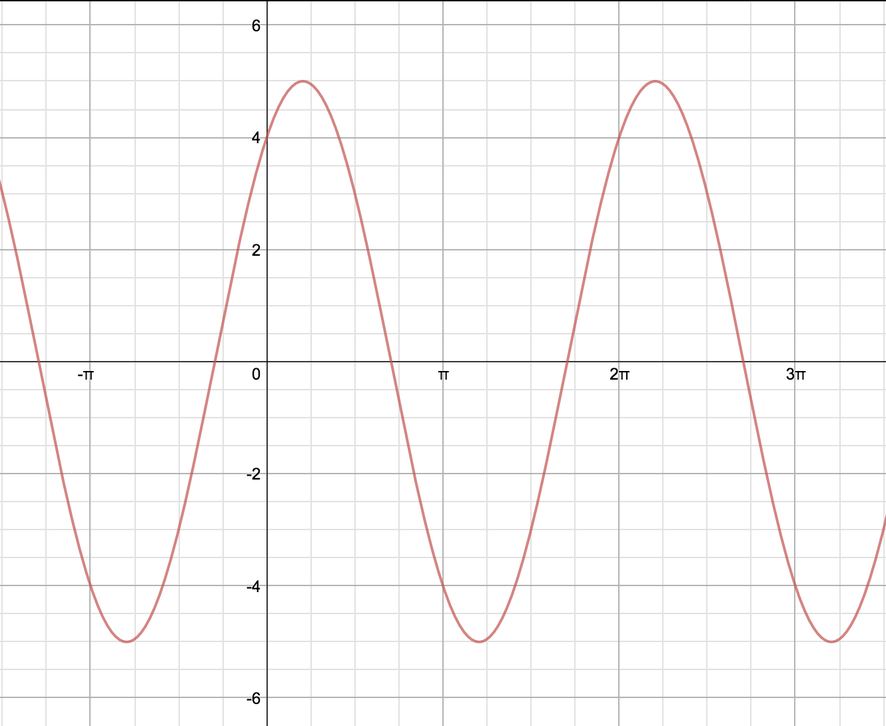
Wave oscillating between y=5 and y=-5 with period 2 Pi. The first positive x-intercept is just before pi and the y-intercept is at 4.

How does this compare with the previous graph?

What function did you use to describe the previous graph?

Below are three graphs of similar functions, namely \[y=A\sin x+B\cos x,\] where \(A\) and \(B\) are real numbers.

Can you work out what \(A\) and \(B\) are for each of these graphs?

Can you describe each of them using a single trigonometric function?

You might want to refer back to Things you might have noticed to help with this.

Graph 1

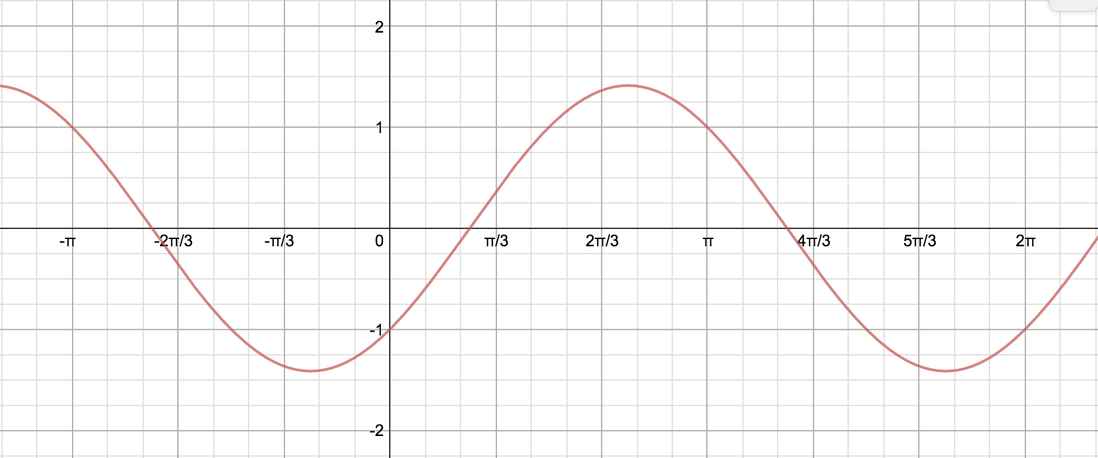
Wave passing through (0,-1) and (pi/2,1)

Graph 2

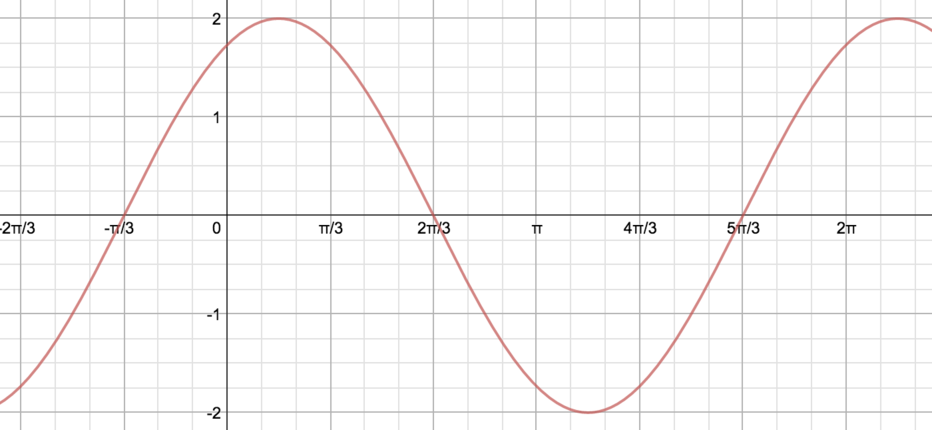
Wave oscillating between y=2 and y=-2, and passing through the points (pi/2,1) and (pi/6,2)

Graph 3

Wave oscillating between y=-2 and y=2 and passing through the points (pi/2,-1), and (pi/6,-2)