The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since \[\sin(x) = \sin(x+360^\circ)\] and \[\cos(x) = \cos(x+360^\circ)\] for all \(x\). With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these videos.
When we first learn about sine and cosine though, it’s in the context of right-angled triangles.
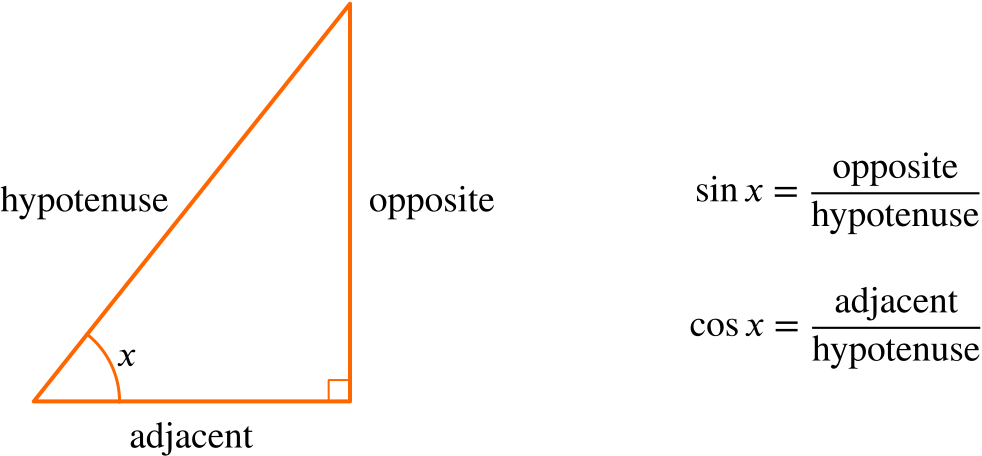
How do the two representations of these two functions fit together?
Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere.

Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle.
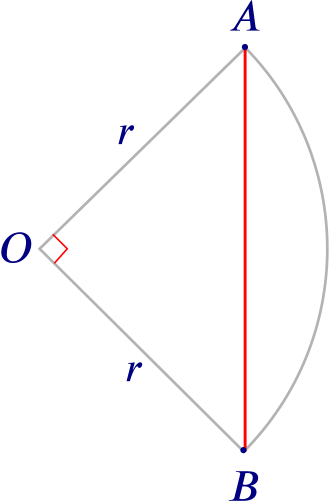
Given two points \(A\) and \(B\) on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle.
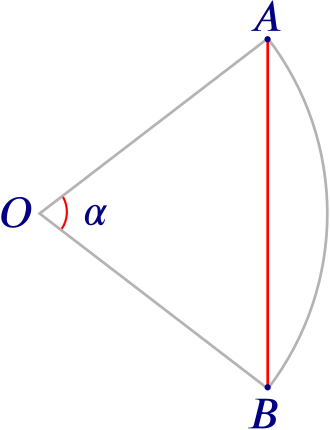
The length of the chord clearly depends on the angle \(\alpha\) formed by the two radii that connect \(A\) and \(B\) to the centre of the circle: for a given circle, the smaller \(\alpha\) is, the smaller the length of the chord will be, provided \(\alpha < 180^{\circ}\). This is true no matter how small or big your circle is. Have a play with the GeoGebra applet below if you need convincing!
To help them with their calculations astronomers produced tables of chords, showing the chord lengths that correspond to given angles. The first person to have written down such a table of chords may have been the Greek astronomer Hipparchus of Nicaea (ca 180BC - ca 125BC). Here are the first few entries in his table of chords:
| \(\alpha^\circ\) | \(0\) | \(7\frac{1}{2}\) | \(15\) | \(22\frac{1}{2}\) | \(30\) | \(37\frac{1}{2}\) | \(45\) | \(52\frac{1}{2}\) |
|---|---|---|---|---|---|---|---|---|
| chord (units) | \(0\) | \(450\) | \(897\) | \(1341\) | \(1779\) | \(2210\) | \(2631\) | \(3041\) |
Hipparchus used a circle of radius \(\approx 3438\) units.
What is the length of the chord when
\(\alpha = 90^\circ\),
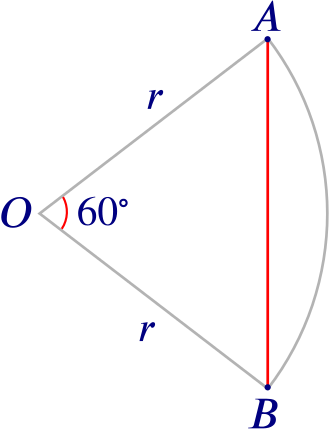
\(\alpha = 60^\circ\)?
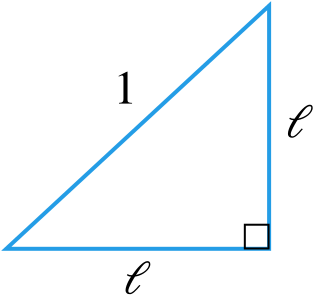
During the 4th and 5th centuries AD, mathematicians and astronomers in India decided that, rather than producing tables to relate chord lengths to angles \(\alpha\), they would produce tables to relate half-chord lengths to half angles \(\alpha/2\). Splitting the angle \(\alpha\) in two gives a right-angled triangle \(T\), with the corners being the centre \(O\) of the circle, the point \(A\) and the mid-point \(M\) of the original chord. The side opposite \(O\) is half the original chord, and the hypotenuse of the triangle is the radius \(r\) of the circle.

What is the length of the half chord?
When Indian mathematicians produced tables relating half angles to half chords, they were effectively producing sine tables. Our modern trigonometric notions reflect their Indian roots. The word “sine” comes from the Sanskrit word for “chord”, jīvā. It was mistakenly transformed into the Arab word jiba which means “bosom” or “fold” and then translated into the Latin word “sinus”.
The definition of sine in terms of right-angled triangles works only for angles \(\alpha/2\) that are less than \(90^\circ\). But there’s a neat way of defining the sine function for angles greater than \(90^\circ\).
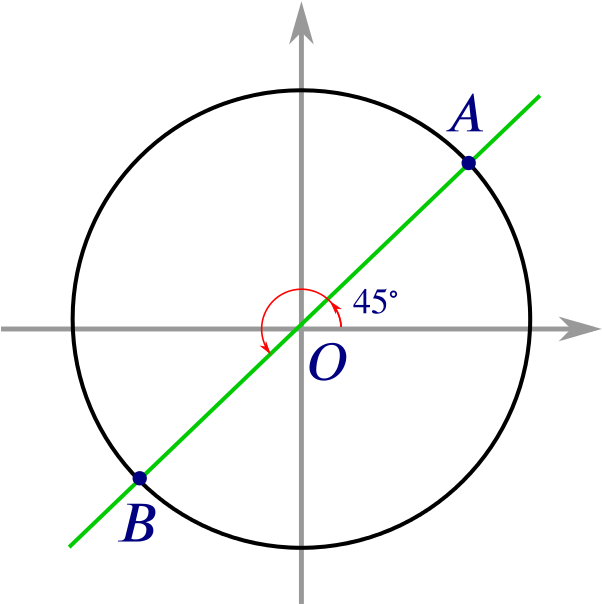
Consider the whole circle on coordinate axes, with its centre at the origin \(O\) and the chord’s midpoint \(M\) lying on the \(x\)-axis. The point \(A\) now has coordinates \((x,y)\), which are both positive. We can assume that the radius of the circle (the hypotenuse of our triangle) is \(1\) and we can also write \(\beta\) (rather than \(\alpha/2\)) for the angle that the triangle subtends at \(O\).
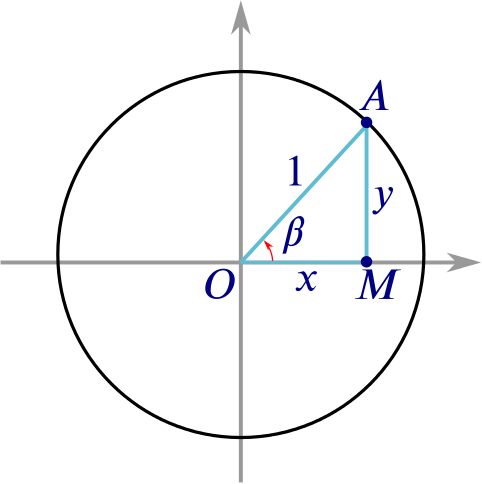
What is the \(y\)-coordinate of the point \(A\)?
What is the \(x\)-coordinate of the point \(A\)?
Now imagine sliding the point \(A\) anti-clockwise around the circle, thereby increasing the angle \(\beta\). We can define \(\sin{\beta}\) to be the \(y\)-coordinate of the corresponding point \(A\) for any value of \(\beta\).
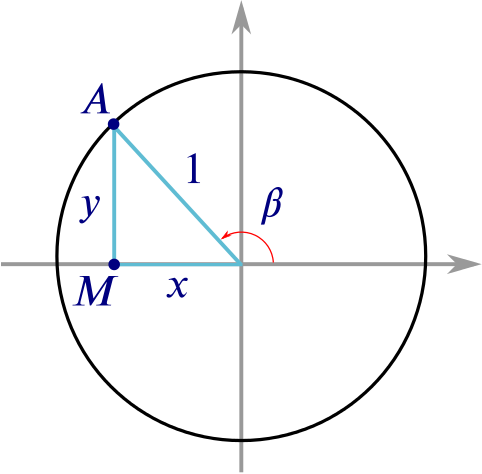
Using the circle, what are the values of
- \(\sin{90^\circ}\),
- \(\sin{180^\circ}\),
- \(\sin{270^\circ}\),
- \(\sin{360^\circ}\)?
We can even define \(\sin \beta\) for angles greater than \(360^\circ\): it’s simply the \(y\)-coordinate of the point you get to when sliding \(A\) round and round the circle in an anti-clockwise direction by \(\beta\), starting with \(A\) sitting at the point \((1,0)\). Similarly, if \(\beta\) is less than \(0^\circ\), we can do the same – this corresponds to \(A\) travelling clockwise from \((1,0)\).
And this is where the waviness of the sine function comes from. As \(A\) moves once around the circle, starting and ending at the point \((1,0)\), its \(y\)-coordinate moves from \(0\) up to a maximum of \(1\) (when \(A\) is at the top of the circle) back down to \(0\) (the leftmost point of the circle), down to \(-1\) (the bottom of the circle) and back up to \(1\), its starting position. Click on the start button below to see an animation of this process.
Another turn around the circle, corresponding to angles between \(360^\circ\) and \(720^\circ\), repeats this single wave segment. A third turn, corresponding to angles between \(720^\circ\) and \(1080^\circ\), gives yet another repeat, and so on.
Something very similar happens for the cosine function. Looking back at the unit circle diagram, for \(A=(x,y)\) in the first quadrant, we see that the usual triangle definition of cosine (as mentioned above) gives \(\cos{\beta} = x.\) Again, as \(A\) moves round the circle in an anti-clockwise direction, we can define \(\cos \beta\) to be the \(x\)-coordinate of \(A\).
The graph of the cosine function has exactly the same wavy shape as that of the sine function, only it is offset by \(90^\circ\) because of the way the \(x\) and \(y\) coordinates of the point \(A\) relate to each other as \(A\) moves around the circle.
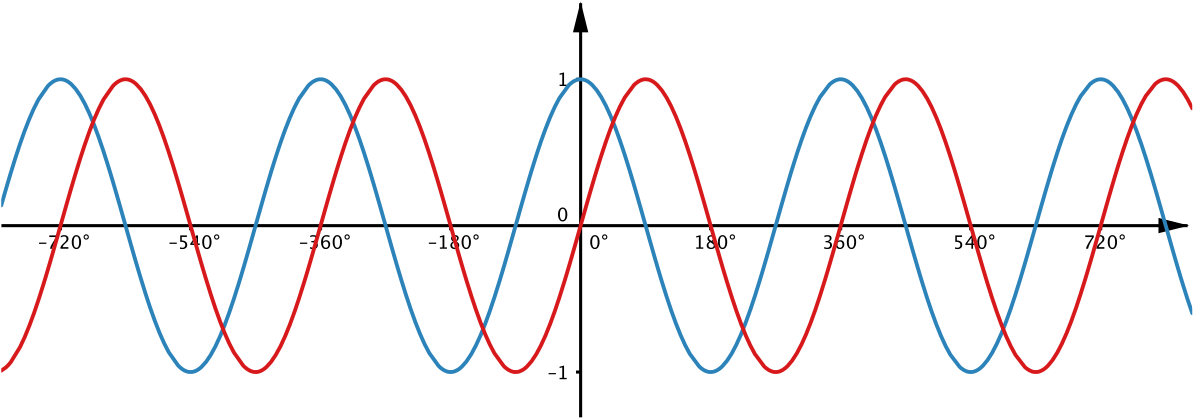
You can see that the waves intersect at certain points.
For what angles do sine and cosine have the same value?
What is the value?
In practice we often solve trigonometry problems using a combination of definitions, i.e. using triangles, the unit circle or graphs. Try to answer this question using these different definitions of sine and cosine.