Given \(\theta\) in the range \(0\leq \theta < \pi\), the equation \[x^2+y^2+4x \cos\theta+8y \sin\theta+10=0\] represents a circle for
\(0<\theta<\dfrac{\pi}{3}\);
\(\dfrac{\pi}{4}<\theta<\dfrac{3\pi}{4}\);
\(0<\theta<\dfrac{\pi}{2}\);
all values for \(\theta\).
This applet shows the curve \(x^2+y^2+4x \cos\theta+8y \sin\theta+10=0\). We can vary \(\theta\) in the range \(0\leq \theta < \pi\).
What happens to the centre and radius of the circle?
By completing the square we obtain \[(x+2 \cos\theta)^2- 4\cos^2\theta+(y + 4\sin\theta)^2-16\sin^2\theta+10=0.\]
Then by rearranging we get \[(x+2\cos\theta)^2+(y+4\sin\theta)^2=4\cos^2\theta + 16\sin^2\theta-10.\]
Since \(\sin^2\theta + \cos^2\theta=1\), we see that the right-hand side becomes \[4\cos^2\theta + 16\sin^2\theta-10 = 12\sin^2\theta-6.\]
So the equation defines a circle of radius \(\sqrt{12 \sin^2\theta-6}\), for \(\sin^2\theta>\dfrac{1}{2}\).
In the range \(0\leq \theta < \pi\), we have \(\sin\theta\geq0\) so we need \(\sin \theta >\dfrac{1}{\sqrt2}\).
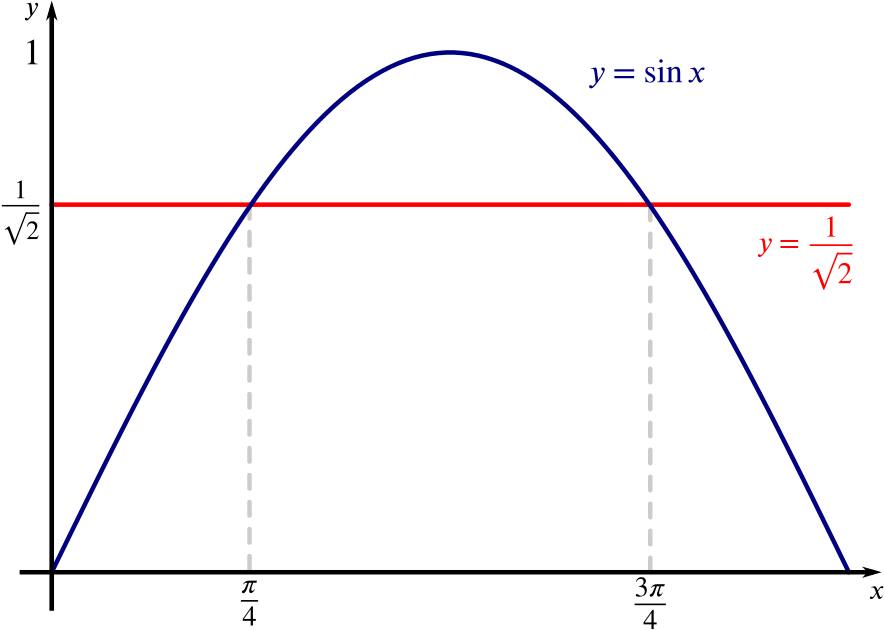
Hence the answer is (b).

