The graph of \(y=\sin x\) is reflected first in the line \(x= \pi\) and then in the line \(y=2\). The resulting graph has equation
\(y=\cos x\);
\(y=2+\sin x\);
\(y=4+\sin x\);
\(y=2-\cos x\).
Approach 1: Sketching graphs
Here is a sketch of \(y=\sin x\), with \(x=\pi\) shown.
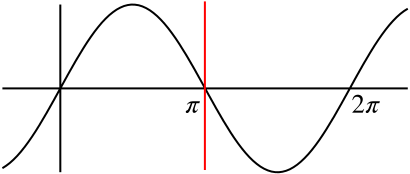
This is what the reflection looks like, with \(y=2\) marked.

This is what the graph looks like once it has been reflected the second time.

It passes through \(4\) on the \(y\)-axis and is clearly a vertical translation of \(y=\sin x\), so the answer must be (c).
Another way to look at it…
Suppose we have two reflections whose mirror lines are not parallel.
If we do one followed by the other, this is equivalent to a rotation about the point where the mirror lines meet.
You could pick some reflections and convince yourself of this.
So here our two reflections are equivalent to a rotation through \(180^\circ\) around \((\pi, 2)\), which takes \(y = \sin x\) to \(y = \sin x + 4\). The answer is (c).
Approach 2: Algebraic transformations
If we reflect \(y = f(x)\) in \(x = a\), we get the curve \(y = f(-x+2a)\).
If we reflect \(y = f(x)\) in \(y = a\), we get the curve \(y = -f(x)+2a\).
When reflected in the line \(x=\pi\), the graph of \(y=\sin x\) becomes \[y=\sin(2\pi -x)=\sin(-x)=-\sin x.\]
When reflected in the line \(y=2\), the graph of \(y=-\sin x\) becomes \[y= 4-(-\sin x)=4+\sin x.\]
The answer is (c).

