Two swimmers cross a river - can we calculate its width?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The above figure shows the parallel banks of a straight stretch of river.

Starting from the point \(A\) on a bank, a man swims at an angle of \(40°\) with the bank, reaching a point \(B\) on the opposite bank after swimming \(150\) yd. A second swimmer also leaves the bank at \(A\) but reaches the opposite bank at \(C\). If \(BC = 50\) yd., calculate

1. the width of the river;

Let’s concentrate on the first swimmer.

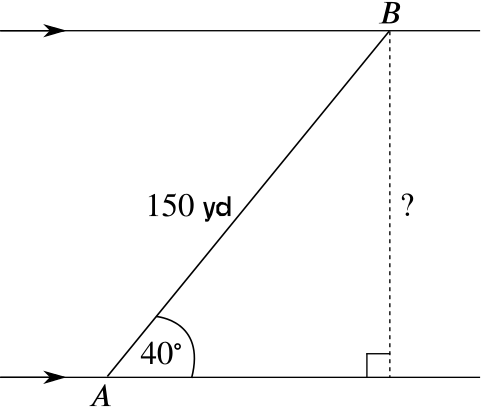
Now we know in a right-angled triangle \(\sin(\theta) = \dfrac{\text{opposite }}{\text{hypotenuse}}\).

For our triangle we have \(\sin 40 = \dfrac{w}{150}\), where \(w\) is the width of the river, which yields \(w = 150\sin 40 \approx 96.4\) yd.

Now let’s think about the second swimmer.

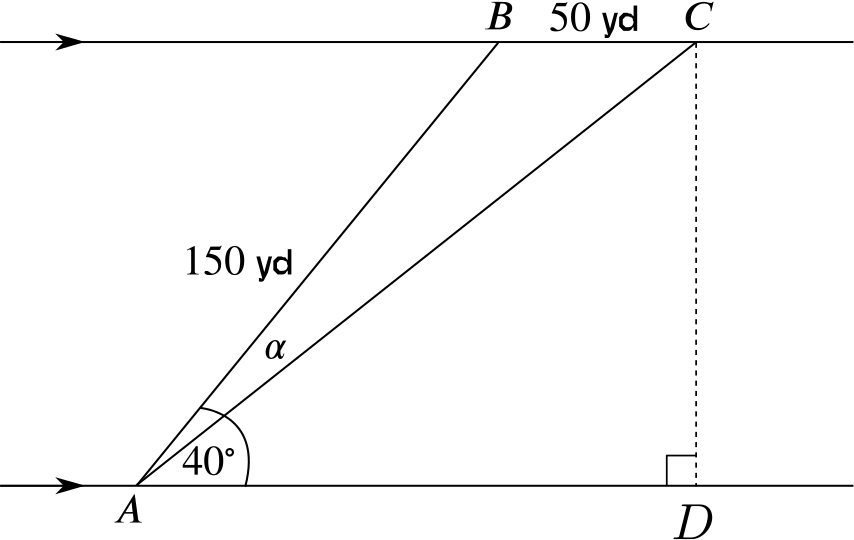
We need to find the angle \(\alpha\). Now \(AD = 150 \cos 40 + 50\), while \(CD = 150\sin 40\), so \(\tan (40-\alpha) = \dfrac{150\sin 40}{150 \cos 40 + 50}\).

Thus \(\tan (40-\alpha) = 0.584683... \implies 40-\alpha = 30.3141... \implies \alpha \approx 9.69^\circ\).