If \(\alpha<\beta\), how many different values are there among the following expressions? \[\sin\alpha\sin\beta \quad \sin\alpha\cos\beta \quad \cos\alpha\sin\beta \quad \cos\alpha\cos\beta\]
Method 1
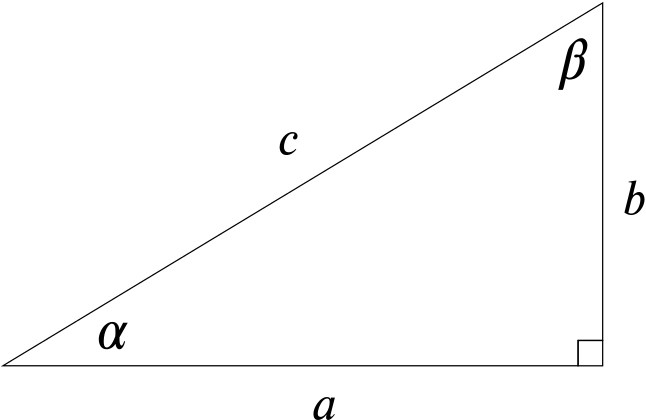
We have
\[\sin\alpha\sin\beta = \frac{b}{c}\frac{a}{c} = \frac{ab}{c^2},\]
\[\sin\alpha\cos\beta = \frac{b}{c}\frac{b}{c} = \frac{b^2}{c^2},\]
\[\cos\alpha\sin\beta = \frac{a}{c}\frac{a}{c} = \frac{a^2}{c^2},\]
and
\[\cos\alpha\cos\beta = \frac{a}{c}\frac{b}{c} = \frac{ab}{c^2}.\]
Now since \(a > b, a^2 > ab > b^2\), and clearly the expressions take exactly three distinct values.
Method 2
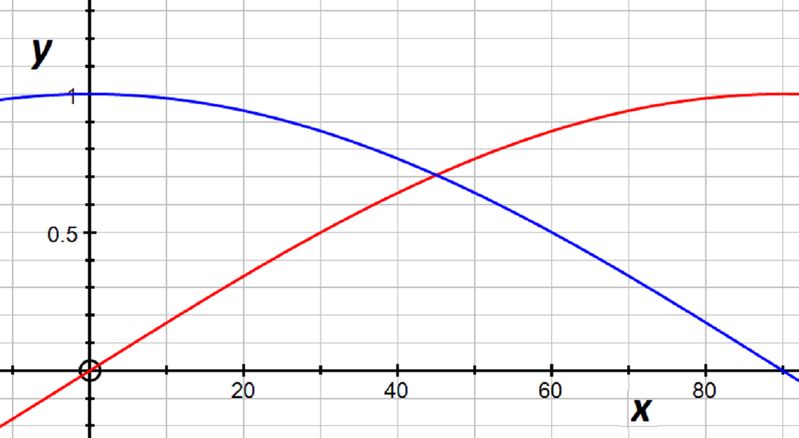
We know that \(0<\alpha<45^{\circ}<\beta<90^{\circ}\). Using the properties of \(\cos\) and \(\sin\) (which which are illustrated in the graph above), we have
\[\begin{align} \sin \alpha < \cos \alpha\label{eq:2}\\ \cos \beta < \sin \beta\label{eq:4}\\ \end{align}\]Now if we start with \(\eqref{eq:4}\) and multiply it by \(\sin\alpha\), we get
\[\sin\alpha\cos \beta < \sin\alpha\sin \beta.\]
If we start with \(\eqref{eq:2}\) and multiply by \(\sin \beta\), we get
\[\sin \beta \sin \alpha <\sin \beta \cos \alpha.\]
Now \(\alpha\) and \(\beta\) are complementary angles, so we can write
\[\cos\alpha\cos\beta=\cos(90^{\circ}-\beta)\cos(90^{\circ}-\alpha)=\sin\beta\sin\alpha.\]
So we can order the four expressions as
\[\sin\alpha\cos\beta<\sin\alpha\sin\beta=\cos\alpha\cos\beta<\cos\alpha\sin\beta\]
and conclude that we have only three different values.

