A road runs from \(A\) due East to \(B\), \(500\) yd. distant. The bearings of a tree from \(A\) and \(B\) are \(048^\circ\) and \(296^\circ\) respectively. Find the distance, correct to the nearest yard, of the tree from the road.
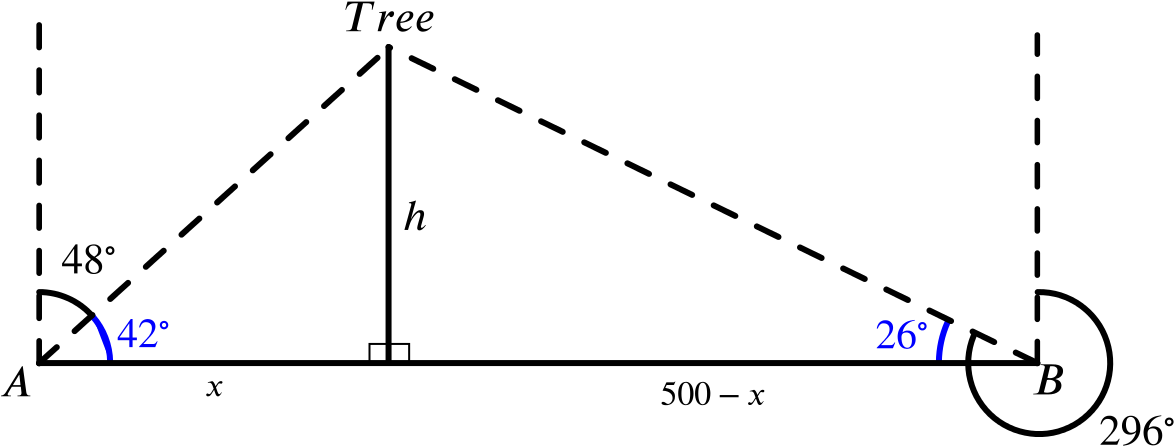
In our diagram, \(h\) represents the perpendicular distance of the tree from the road and \(x\) is the distance from the foot of the perpendicular to \(A\).
From the left hand triangle, we find that \[\begin{equation}\label{eq:1} \tan 42^\circ=\frac{h}{x}, \end{equation}\] and from the right hand triangle, \[\begin{equation}\label{eq:2} \tan 26^\circ=\frac{h}{500-x}. \end{equation}\]Rearranging equation \(\eqref{eq:1}\), we find that \(x=\dfrac{h}{\tan 42^\circ}\). Substituting this into \(\eqref{eq:2}\), we find that \[\tan 26^\circ=\frac{h}{500-\dfrac{h}{\tan 42^\circ}}.\] Rearranging, we find that \[h\left(1+\frac{\tan 26^\circ}{\tan 42^\circ}\right)=500\tan 26^\circ,\] and so \[h=\frac{500\tan 26^\circ}{1+\dfrac{\tan26^\circ}{\tan42^\circ}}.\]
This gives us that \(h=158\) yd. to the nearest yard.

