Show that the perpendicular distance of the point \((h,k)\) from the straight line \(x\cos\alpha+y\sin\alpha=p\) is the numerical value of \[h\cos\alpha+k\sin\alpha-p.\] [“Numerical value” means ignoring whether it is positive or negative, that is, the absolute value of this expression.]
Two approaches to this question are given here; the first approach comes to mind more quickly, perhaps, but the second approach works for any value of \(\alpha\).
Approach 1
We begin by sketching the line \(x\cos\alpha+y\sin\alpha=p\), and finding the points of intersection with the \(x\) and \(y\) axes.
By substituting \(x=0\) into the equation of the line, we get that the line intersects the \(y\)-axis at \(y=\dfrac{p}{\sin\alpha}\). Similarly, the line intersects the \(x\)-axis at \(x=\dfrac{p}{\cos\alpha}\).
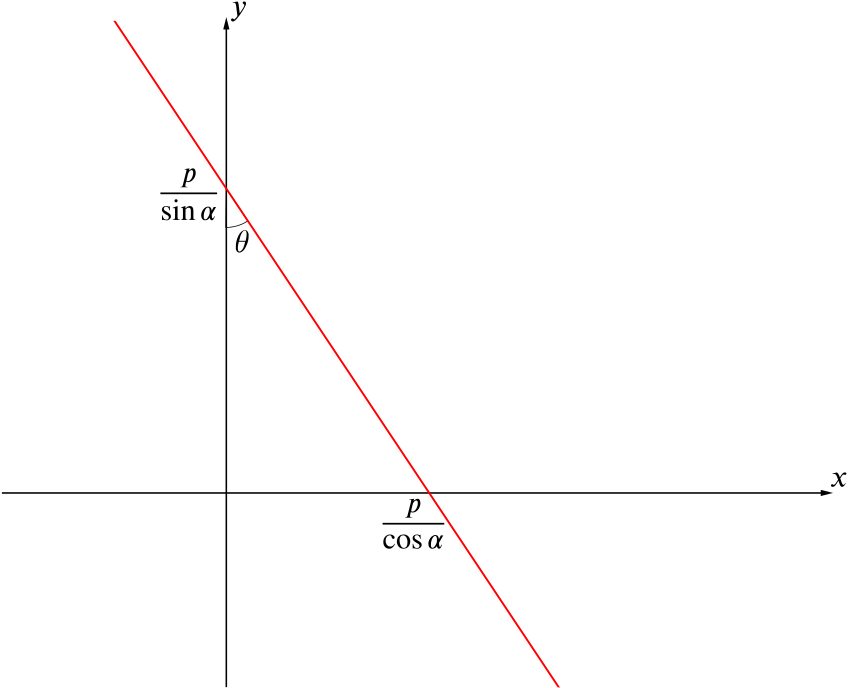
We may have wondered up until now about the significance of our constant \(\alpha\) and if it represents any of the angles in our diagram. Consider the angle \(\theta\), as shown in the diagram above. We know that
\[\tan \theta = \frac{\text{opposite}}{\text{adjacent}} = \frac{\left(\frac{p}{\cos\alpha}\right)}{\left(\frac{p}{\sin\alpha}\right)} = \frac{\sin \alpha}{\cos \alpha} = \tan \alpha.\]
This now tells us that \(\theta = \alpha\).
Does this argument still work in the case where \(\alpha\) is obtuse or reflex? Will our angle \(\theta\) still be equal to \(\alpha\) in this case?
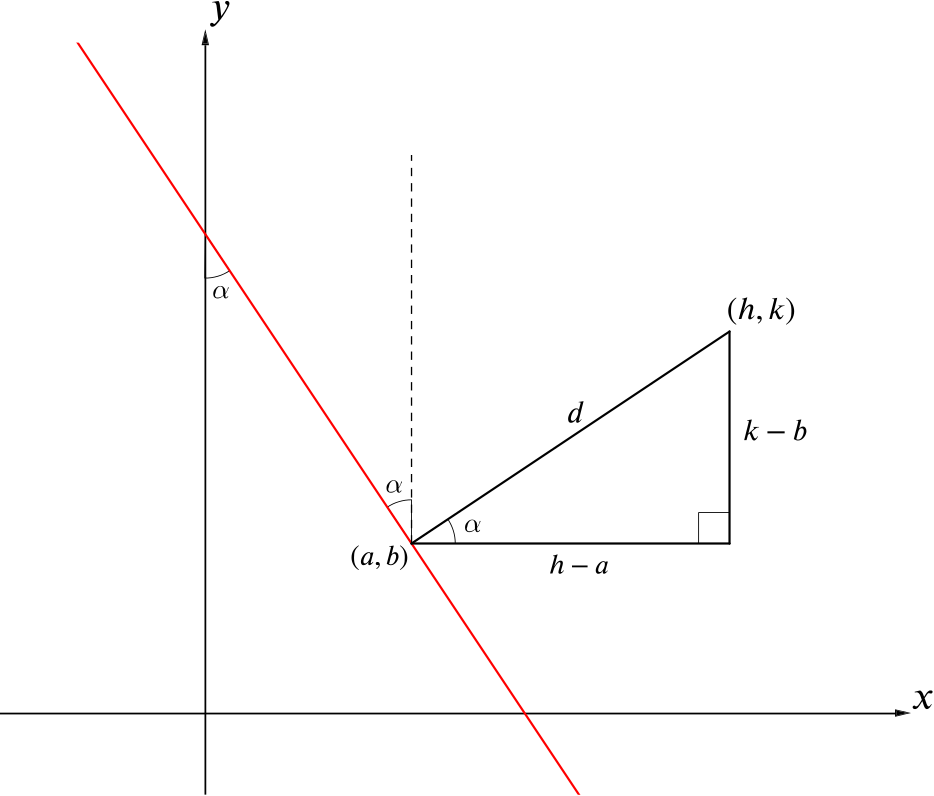
We’ll label the perpendicular distance from the point \((h,k)\) to the line \(d\), and the point of intersection \((a,b)\) (we’ll assume that \((h,k)\) is on the opposite side of the line to the origin).
By alternate angles, we know that the angle between the line and the vertical at \((a,b)\) is \(\alpha\), and hence the angle between the perpendicular line and the horizontal must also be \(\alpha\).
By considering the right-angled triangle in the diagram above, we see that
\[\cos\alpha=\frac{h-a}{d} \quad \text{and} \quad \sin\alpha=\frac{k-b}{d}\]
which we can rearrange to give
\[a=h - d \cos\alpha \quad \text{and} \quad b=k-d\sin\alpha.\]
As \((a,b)\) is a point on the line, we know that \(a\cos\alpha+b\sin\alpha=p\) and so
\[(h - d \cos\alpha)\cos\alpha+(k-d\sin\alpha)\sin\alpha=p\]
which rearranges to
\[h \cos\alpha + k \sin\alpha - p = d(\sin^2 \alpha + \cos^2 \alpha) = d,\]
as required.
If \((h,k)\) was on the same side of the line as the origin, in what ways would our calculations change?
Approach 2
We’ll begin by considering our original diagram; we’ve found the significance of \(\alpha\), can we find the significance of \(p\) as well?
Can we find the perpendicular distance of the line from the origin? The intercepts are proportional to \(p\), so it’s reasonable to think that this distance will be too.
So adding in this line, we can see a right-angled triangle with angle \(\alpha\) and hypotenuse \(\dfrac{p}{\sin \alpha}\).
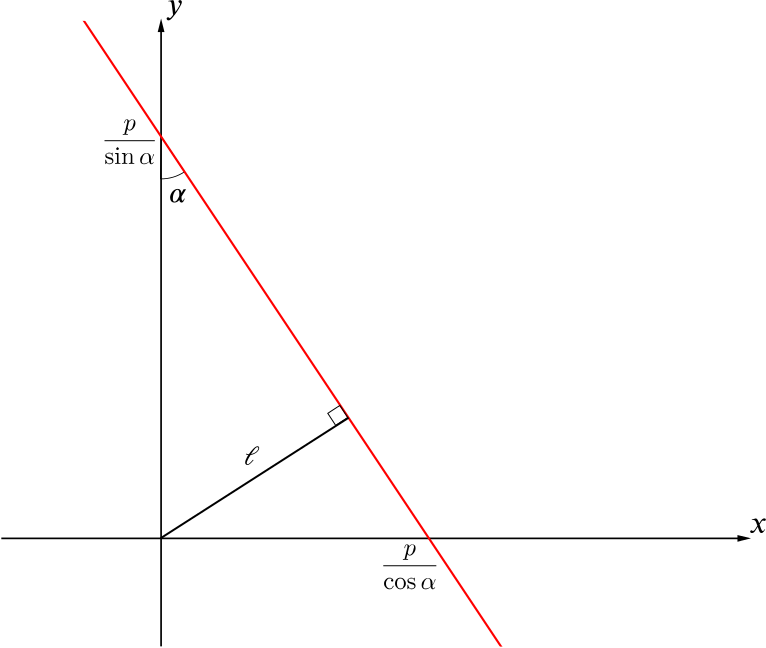
Letting \(\ell\) be the length of the perpendicular line, we see that
\[\sin\alpha = \frac{\ell}{\left(\frac{p}{\sin\alpha}\right)} \]
and rearranging gives us
\[ \ell = p.\]
Therefore \(p\) represents the perpendicular distance of the line from the origin.
With our new result \(\ell = p\) in mind, we now consider the line passing through \((h,k)\) and parallel to our original line.
By our result above, the equation of this line is \(x\cos\alpha+y\sin\alpha=q\), where \(q\) is the perpendicular distance from the line to the origin.
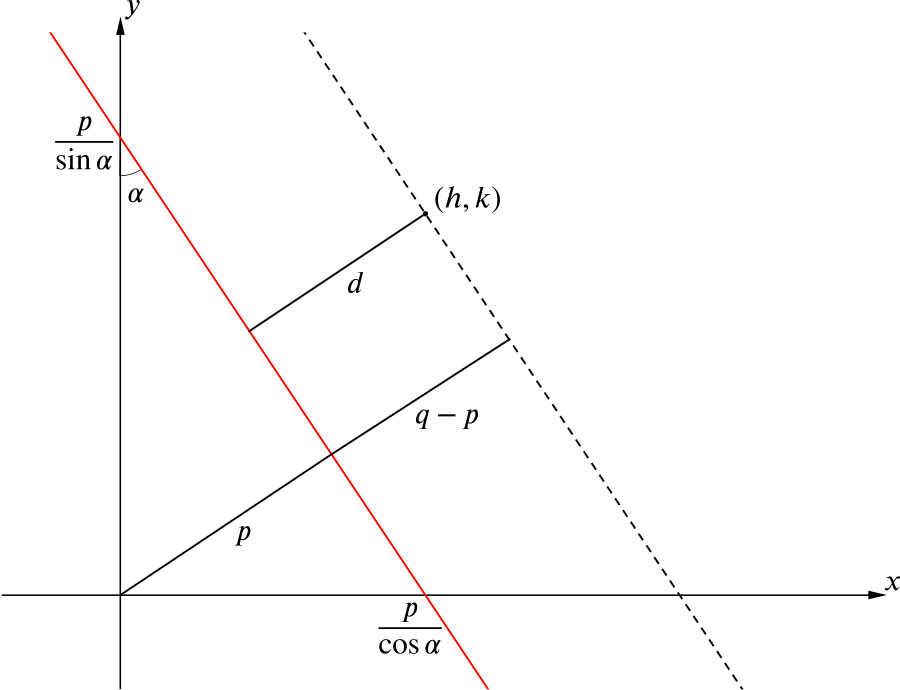
We can see that the perpendicular distance from the original line to the point \((h,k)\) is equal to the difference between the two perpendicular distances from the origin.
We can write this as \(|q-p|\) to account for the case where \(p>q\), i.e. the case where \((h,k)\) is on the other side of the line.
As \((h,k)\) is a point on the line, this can be rewritten as
\[d = |h \cos\alpha + k \sin\alpha - p|.\]
Would our conclusion still be the same if \(p\) was negative?
It may be worth taking a step back and thinking about the two approaches we have just seen.
Which one do you prefer? Does one or the other provide more insight to the result?
Calculate the coordinates of the centres of the two circles of radius \(5\) which pass through the point \((4,4)\) and touch the straight line \(3x-4y-28=0\).
We need to find the points that are a distance of \(5\) away from \((4,4)\), and which have perpendicular distance \(5\) from the line \(3x-4y-28=0\).
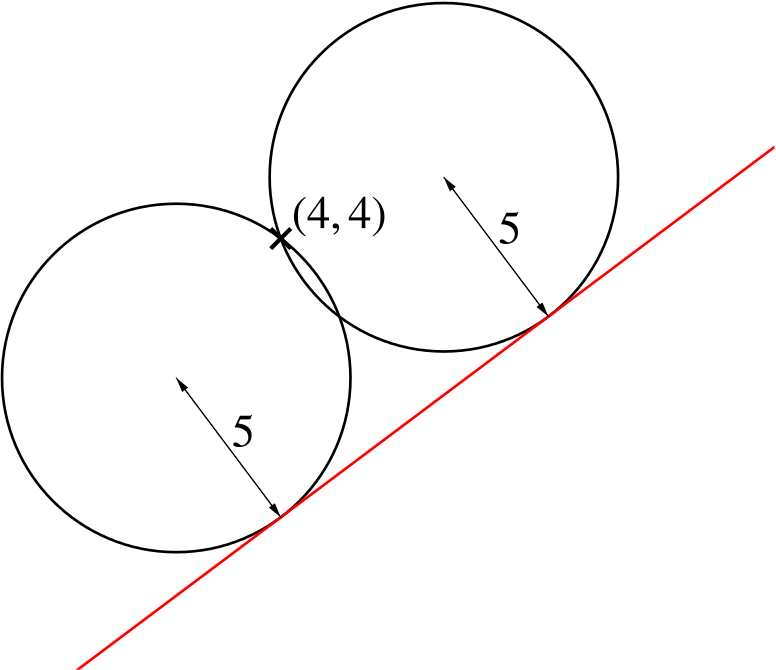
We can use the formula for distance that we have just found.
The line we’ve been given is not quite in the form we require, since \(3\) and \(-4\) cannot be the values of \(\cos\alpha\) or \(\sin\alpha\).
But we can scale the whole equation by a real positive number \(r\). We multiply through to get \[3rx-4ry-28r = 0\] which gives \[3r=\cos\alpha, -4r=\sin\alpha.\] Dividing these gives \(\tan \alpha =-\dfrac{4}{3}\), which means \(\alpha\) is a reflex angle (this wasn’t explicitly dealt with above, but our argument can accommodate this without too much trouble).
Since \(\sin^2\alpha+\cos^2\alpha=1\) we see that \(9r^2+16r^2=1\), so \(r=\dfrac{1}{5}\). We can write the line as \[\frac{3}{5}x-\frac{4}{5}y-\frac{28}{5}=0,\] so \(\cos\alpha=\dfrac{3}{5}\), \(\sin\alpha=-\dfrac{4}{5}\), and \(p=\dfrac{28}{5}\).
The perpendicular distance from \((4,4)\) to the line is \[\left|\frac{3}{5} \times 4 - \frac{4}{5}\times4-\frac{28}{5}\right|=\left|\frac{-4-28}{5}\right|=\frac{32}{5} > 5.\]
Let \((h,k)\) denote the coordinates we are trying to find. Note that we need to find two possible options for \((h,k)\).
The perpendicular distance between \((h,k)\) and the given line is \[\left|\frac{3}{5}h-\frac{4}{5}k-\frac{28}{5}\right|=5.\]
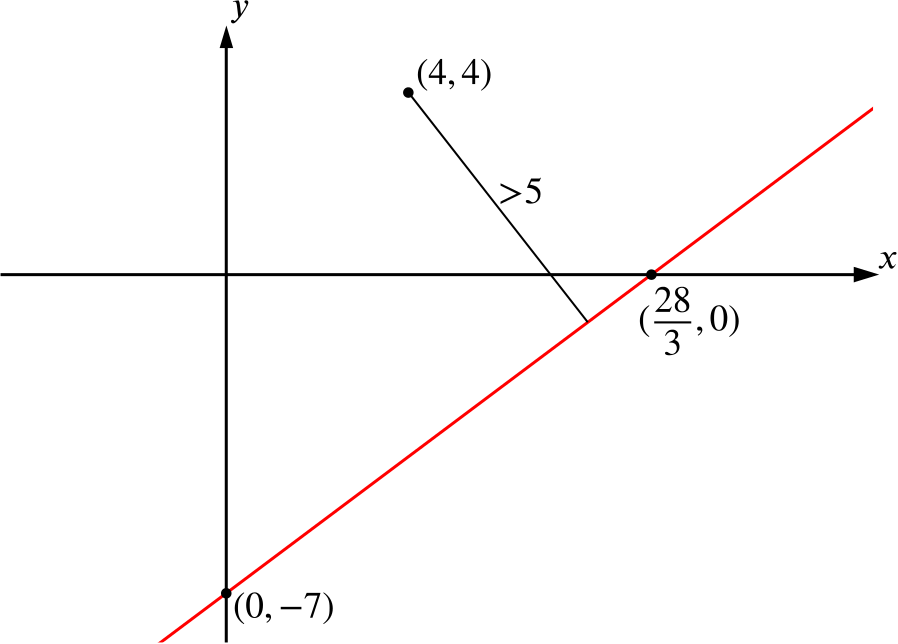
From our sketch we can see that \((4,4)\) is on the same side of the line as the origin, and so the points \((h,k)\) we seek must be the same side of the line as the origin also.
How far are our centres \((h,k)\) from the line? We have \[\frac{3}{5}h-\frac{4}{5}k-\frac{28}{5}=-5\] (we must have -5 here, since we are on this side of the line) which is equivalent to \[h=1+\frac{4}{3}k.\]
Since the distance between \((h,k)\) and \((4,4)\) is \(5\), we also know that \(5=\sqrt{(h-4)^2+(k-4)^2}\), and substituting for \(h\) we obtain \[5=\sqrt{\left(\frac{4}{3}k-3\right)^2+(k-4)^2}\] which can be rearranged to give the quadratic \[0 = 25k^2-144k = k(25k - 144),\] which is satisfied for \(k=0\), and \(k=\dfrac{144}{25}\).
So we have the two points \((1,0)\) and \(\left(\dfrac{217}{25},\dfrac{144}{25}\right)\) as the centres of our two circles.

